フーリエの法則と熱伝導(伝導伝熱) 平板・円筒・球での熱伝導度(熱伝導率)の計算方法
このページでは、熱伝導(伝導伝熱)の基礎法則であるフーリエ(Fourrier)の法則や
平板、円筒壁、中空球壁モデルにおける伝導速度について解説しています。
伝熱の仕方(熱の伝わり方)の種類はこちらで解説しています。
フーリエ(Fourrier)の法則と熱伝導
伝導伝熱(熱伝導)は物質の分子や原子レベルでの、並進、回転、振動といった熱運動のエネルギーの伝搬による熱の伝わり方のことを言います。
伝導伝熱は以下のフーリエ(Fourrier)の法則に従い、熱が伝わります。

このkを熱伝導度、もしくは熱伝達率と呼びます。
熱流束は温度勾配(dT/dx)、熱伝導度に比例するという法則です。
面積を考慮した場合のフーリエ(Fourrier)の法則は以下のようになります。
Q = - A k dT/dx
Q:(伝熱量[W])、A:伝熱面積
熱伝導度は物質により異なり、一般的に固体>液体>気体の順番になります。
熱を速く伝えたい、もしくは逃がしたい場合には、熱伝導度が大きい金属等を使用したり、逆に熱を伝えたくない、もしくは逃がしにくくしたい場合にはグラスウール等の断熱材や空気の層を入れる等、熱設計によって熱伝導度の大小を考慮します。
ちなみに上述しましたが、空気も熱伝導度が0.026程度と非常に低く、熱を逃がしにくいのです。
関連記事
対流伝熱とは?
放射伝熱とは?
熱交換器の計算問題を解いてみよう
熱伝導率の測定方法(簡易)は?
フィックの法則(拡散現象の公式)とは?
熱流束(熱フラックス)とは?
平板での熱伝導
最もシンプルなモデルである、平板の伝熱速度と温度分布について以下の問題で考えていきましょう。
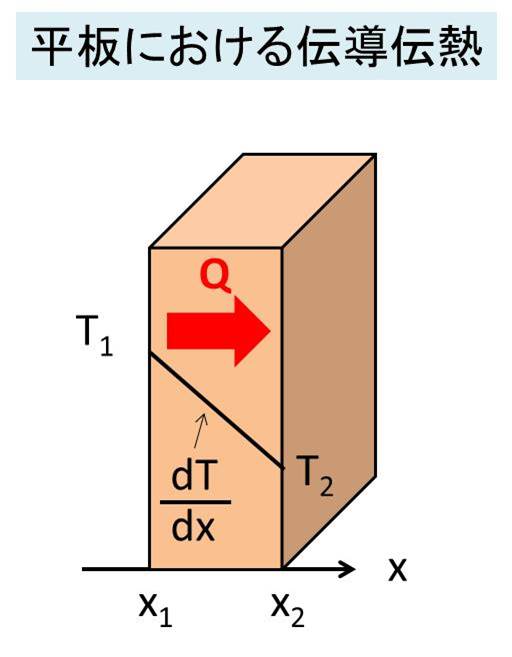
左面をT1(高温)℃、右面をT2(低温)℃、断面積をA m2、厚みをl = x2 - x1 mとします。
定常状態では、上記のよう温度勾配が直線になります。
フーリエの法則を用いて下記のよう,式変形していきます。
すると定常状態における伝熱速度が平板の定常状態におけるパラメータ(表面温度、厚み、断面積)から算出することができます。

平板における定常状態の伝熱速度は非常にシンプルですね。きちんと熱伝導の求め方を理解しましょう。
関連記事
対流伝熱とは?
放射伝熱とは?
熱交換器の計算問題を解いてみよう
熱伝導率の測定方法(簡易)は?
フィックの法則(拡散現象の公式)とは?
熱流束(熱フラックス)とは?
円筒壁での伝導伝熱
次に、配管の熱設計を行う場合などに利用される円筒壁での伝導伝熱(熱伝導)について、解説します。
基本的な考え方は平板の伝導伝熱と同じですが,、円筒壁の場合は内壁と外壁の表面積が異なるため、
温度勾配が直線になりません。
そのため、上述した平板における伝熱速度の導出説明において、
・x→rに置き換えること
・面積Aに対数平均面積Aを使用すること
が異なります。
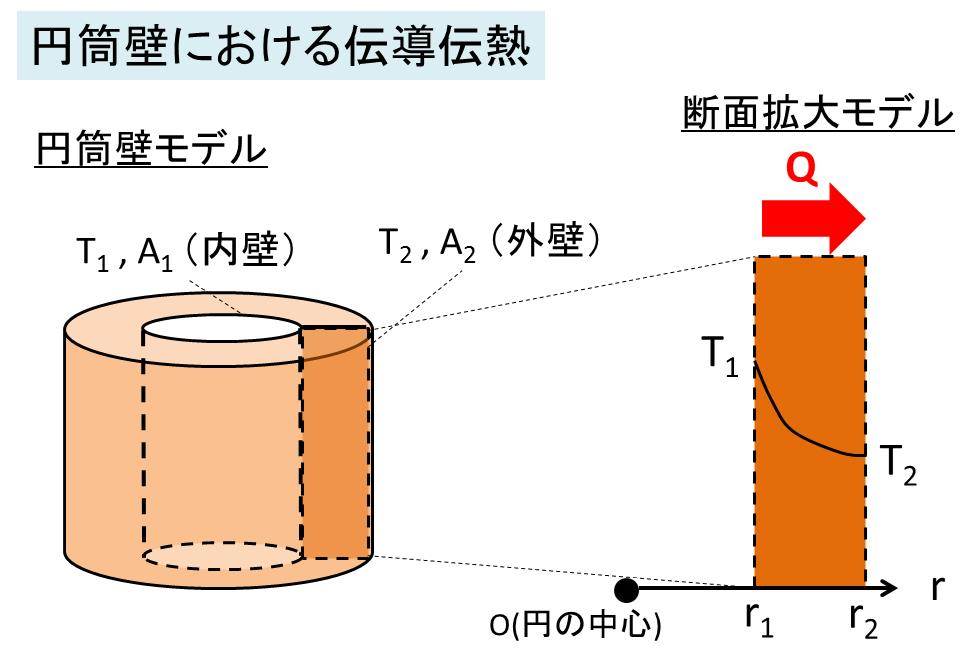
復習も兼ね、x→r、Aに対数平均面積を使用した場合の伝導伝熱の式の導出を以下に記載します。

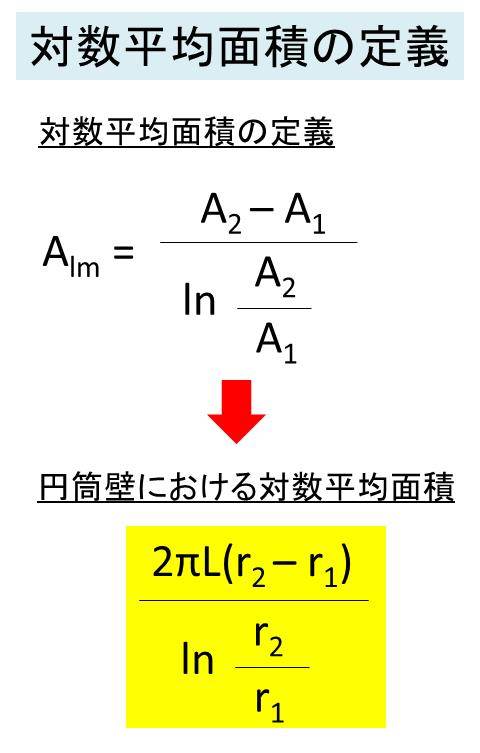
上記式で使用している対数平均面積の定義を下記に示します。(熱交換器の計算問題における対数平均温度差とは異なりますので、気を付けましょう)
関連記事
対流伝熱とは?
放射伝熱とは?
熱交換器の計算問題を解いてみよう
熱伝導率の測定方法(簡易)は?
フィックの法則(拡散現象の公式)とは?
熱流束(熱フラックス)とは?
中空球壁における伝熱速度(熱流束)
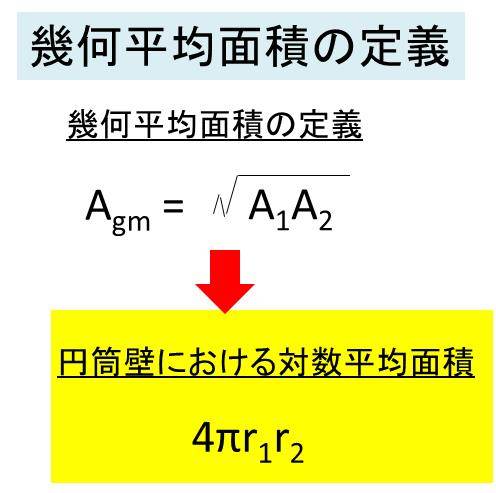
こちらも、平板や円筒壁における伝熱と伝熱速度の導出仮定は同じであり、中空球壁では面積Aに幾何平均面積を使用することが異なります。(Qの式は円筒壁形状と同じであり、使用するAのみが異なります。)
中空球壁における伝導伝熱のモデルを下記に示します。
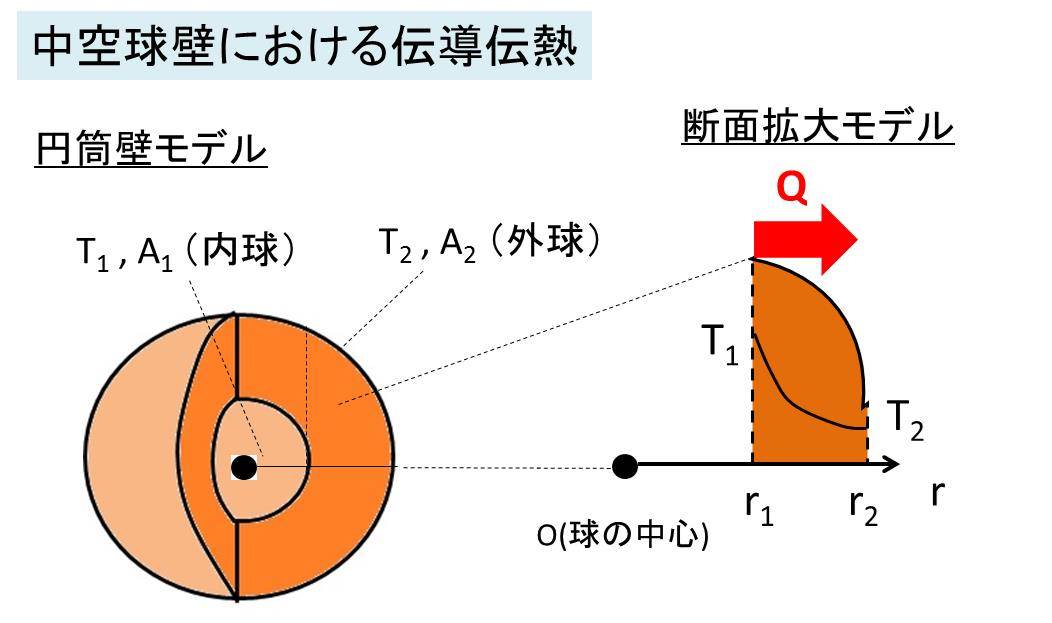
最後に、中空球壁における伝導伝熱で使用する
幾何平均面積の定義を示します。
関連記事
対流伝熱とは?
放射伝熱とは?
熱交換器の計算問題を解いてみよう
熱伝導率の測定方法(簡易)は?
フィックの法則(拡散現象の公式)とは?
熱流束(熱フラックス)とは?
フーリエの法則と熱伝導(伝導伝熱) 平板・円筒・球での熱伝導度(熱伝導率)の計算方法 関連ページ
- 熱の伝わり方(伝熱の仕方)の種類
- 多層平板における熱伝導(伝導伝熱)と伝熱抵抗 熱伝導度の合成
- ニュートン冷却の法則や総括伝熱係数(熱貫流率・熱通過率)とは?【対流伝熱】
- ニュートン粘性の法則の導出と計算方法 ニュートン流体と非ニュートン流体とは?【粘性係数(粘性率)と速度勾配】
- 放射伝熱(輻射伝熱)とは?プランクの法則・ウィーンの変位則・ステファンボルツマンの法則とは?
- 熱交換器の計算問題を解いてみよう 対数平均温度差(LMTD)とは?【演習問題】
- 比熱の測定方法(簡易版)
- 熱伝導率の測定・計算方法(定常法と非定常法)(簡易版)
- 熱拡散率(温度拡散率)と熱伝導率の変換・計算方法【演習問題】
- 反応速度と定常状態近似法、ミカエリス・メンテン式
- ラウールの法則とは?計算方法と導出 相対揮発度:比揮発度とは?【演習問題】
- 蒸気圧と蒸留 クラウジウス-クラペイロン式とアントワン式
- 流速と流量の計算・変換方法 質量流量と体積流量の違いは?【演習問題】
- 流束と流束密度の違いは? 流束と流束密度の計算問題を解いてみよう【演習問題】
- 流速と流束(フラックス)の違いは? 流束の種類
- レイノルズ数、ファニングの式とは?導出方法と計算方法【粘性力と慣性力の比】
- 単蒸留とは?レイリーの式の導出と単蒸留の図積分を用いた計算問題【演習問題】
- フラッシュ蒸留と単蒸留とフラッシュ蒸留の違いは?【演習問題】
- 連続蒸留とは?蒸留塔の設計における理論段数・最小還流比とは?【演習問題】
- 蒸留塔における理論段数の算出方法(McCabe-Thiele法による作図)は?理論段数・最小還流比とは?【演習問題】
- ベルヌーイの定理とは?ベルヌーイの定理の問題を解いてみよう【演習問題】
- 反応器(CSTRとPFR)の必要体積の比較の問題【反応工学の問題】
- 逐次反応 複合反応の導出と計算【反応工学】
- 並列反応 複合反応の導出と計算【反応工学】
- 転化率・反応率・選択率・収率 導出と計算方法は?【反応工学】
- 平均滞留時間 導出と計算方法【反応工学】
- 反応次数の計算方法 0次・1次・2次反応【反応工学】
- 粒子の沈降とは?ストークスの法則(式)と終末速度の計算方法【演習問題】
- 含水率とは?湿量基準含水率と乾量基準含水率の違いは?
- 参考文献
- ヌッセルト数(ヌセルト数)・グラスホフ数・プラントル数
- レイリー数(レーレー数)とは?
- U字管マノメーターの原理と計算方法
- 層流・乱流・遷移領域とは?層流と乱流の違い
- 熱伝導率と熱伝達率の違い【熱伝導度や熱伝達係数との違い】
- フィックの法則の導出と計算【拡散係数と濃度勾配】
- 熱抵抗を熱伝導率から計算する方法【熱抵抗と熱伝導率の違い】
- 【ハ-ゲンポアズイユの定理】円管における層流の速度分布を計算する方法
- 質量保存則と一次元流れにおける連続の式 計算問題を解いてみよう【圧縮性流体と非圧縮性流体】
- 静圧と動圧の違い【位置エネルギーと運動エネルギー】
- ゲージ圧力と絶対圧力の違いは?変換(換算)の計算問題を解いてみよう【正圧と負圧の違いは?】
- 熱流束・熱フラックスを熱量、伝熱量、断面積から計算する方法【熱流束の求め方】