粒子の沈降とは?ストークスの法則(式)と終末速度の計算方法【演習問題】
当サイトでは、リチウムイオン電池をメインテーマとして各種解説をしていますが、リチウムイオン電池だけでなく、製造業において化学工学の知識は不可欠です。
例えば、リチウムイオン電池の製造工程としては、電極スラリーを混練する際の撹拌する力や与えるエネルギーの設計、電極スラリーを混練したあとの電極基材へ塗布した後のコーターでの乾燥条件の設計などに化学工学の知識が必要になる場合があります。
他にも正極・負極活物質は粉体であり、粉体をふるい分けたり濃縮したりする際の設計にも、化学工学が必要です。
ここでは、化学工学における基礎技術である「分級分離や濃縮技術」の中でも重要な粒子の沈降について解説していきます。
・粒子の沈降とは?ストークスの法則と終末速度
・終末速度を計算してみよう 粒子の沈降の計算問題【演習問題】
というテーマで解説しています。
粒子の沈降とは?ストークスの法則と終末速度
粒子の沈降とは、ある溶媒中に、溶媒にとけない粒子を入れた際に徐々に沈んでいく現象のことを指します。
粒子の沈降速度について、粒子を一つとりだしある液体中にいれたときの、沈降速度を以下で考えていきましょう。
まず、粒子一粒が受ける力について考えていきます(浮力の考え方をもとに式を立てましょう)。
下図のように、粒子には重力による力と浮力による力が働きます。
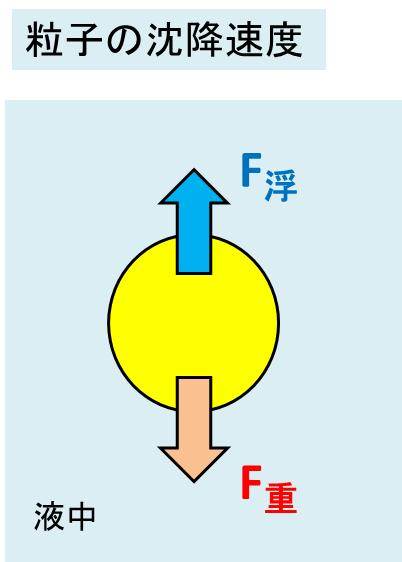
ここで、粒子の質量をm[kg]、重力加速度をg[m/s^2]、粒径をD[m]、粒子の密度をρ粒[kg/m^3]、液体の密度をρ液[kg/m^3]とします。
すると、F重=mg となり、これろ粒径などを用いた式に変形すると、F重=π・D^3・ρ粒・g / 6となります。
一方浮力は、液体の密度×排除体積であるため、F浮=π・D^3・ρ液・g / 6となります。
ここで、沈降速度を考える際は沈降する方向を正と考え、こちらの向きに働く力のことを有効重力と呼びます。
有効重力W = F浮 ー F重 = (π・D^3・g / 6)(ρ粒-ρ液)となります。
さらに加えて、沈降するときには抵抗力を液体からうけます。この抵抗力 R抵 は「粒子のレイノルズ数Re(粒)をまず算出し、2より小さいときに後程解説の式が成立する」というものです。
粒子のレイノルズ数Re(粒)は以下の式で求められます。

終末速度とは粒子の沈降が進み、加速される中で抵抗力が大きくなると有効重力とつりあうようになり、このときの一定となった速度のことを指します。
基本的にはこの粒子のレイノルズ数が2以下では、抵抗力の概算値が以下のストークスの抵抗法則に従うとします。
ただ、計算の手順としては、「一旦ストークスの抵抗法則で抵抗値を計算し、終末速度を計算したのちに、粒子のレイノルズ数が2以下かどうかを判定する」という流れが基本です。
以下がストークスの抵抗法則における粒子の沈降時の抵抗の計算方法です。

この式におけるvは終末速度を表しています。
さらに、終末速度は有効重力とストークスの法則における抵抗値がつりあうときの値であるため、有効重力=抵抗力という式を解くことによって、導出することができます。
以下の通りです。

ただ、先にも述べたように粒子のレイノルズ数が2以下のときのみに成立する式です。
理解を深めるために以下の計算問題を解いてみましょう。
関連記事
リチウムイオン電池の製造工程とは?
電極スラリーとは?
レイノルズ数とは?計算方法は?
浮力とは?浮力の計算方法は
終末速度を計算してみよう 粒子の沈降の計算問題【演習問題】
例題
粒径が0.5mmの玉を、粘度が2.5P・sで比重が2g/cm^3の液体中の沈降させたとします。
玉の材質は鉄であり、その比重が8g/cm^3であるときの終末速度を計算してみましょう。
解答
先ほど導出した終末速度の定義に従って、終末速度を求めていきましょう。

V=(8 - 2) × 10^3 × 9.8 × (5 × 10^-4)^2 / (18 × 2.5) = 3.27 × 10^-4 m/sと算出できました。
ここで、粒子のレイノルズ数が2以下となっているかどうかを確認しましょう。
Re=Dv/µに代入して、 5 × 10^-4 × 3.27 × 10^-4 / 2.5 = 6.5 × 10^-8 と2より大幅に小さいことを確認できたため、上の終末速度であると判断できます。
ちなみに粒子ではない形状のものも、終末速度を測定し上の式に当てはめDを算出することで、粒子形状でなくてもそれに相当する大きさに換算することができます。このときの径Dををストークス径とよびます。
計算式がわからなくなっても導出できるように過程をきちんと理解するといいです。
関連記事
リチウムイオン電池の製造工程とは?
電極スラリーとは?
レイノルズ数とは?計算方法は?
浮力とは?浮力の計算方法は
粒子の沈降とは?ストークスの法則(式)と終末速度の計算方法【演習問題】 関連ページ
- 熱の伝わり方(伝熱の仕方)の種類
- フーリエの法則と熱伝導(伝導伝熱) 平板・円筒・球での熱伝導度(熱伝導率)の計算方法
- 多層平板における熱伝導(伝導伝熱)と伝熱抵抗 熱伝導度の合成
- ニュートン冷却の法則や総括伝熱係数(熱貫流率・熱通過率)とは?【対流伝熱】
- ニュートン粘性の法則の導出と計算方法 ニュートン流体と非ニュートン流体とは?【粘性係数(粘性率)と速度勾配】
- 放射伝熱(輻射伝熱)とは?プランクの法則・ウィーンの変位則・ステファンボルツマンの法則とは?
- 熱交換器の計算問題を解いてみよう 対数平均温度差(LMTD)とは?【演習問題】
- 比熱の測定方法(簡易版)
- 熱伝導率の測定・計算方法(定常法と非定常法)(簡易版)
- 熱拡散率(温度拡散率)と熱伝導率の変換・計算方法【演習問題】
- 反応速度と定常状態近似法、ミカエリス・メンテン式
- ラウールの法則とは?計算方法と導出 相対揮発度:比揮発度とは?【演習問題】
- 蒸気圧と蒸留 クラウジウス-クラペイロン式とアントワン式
- 流速と流量の計算・変換方法 質量流量と体積流量の違いは?【演習問題】
- 流束と流束密度の違いは? 流束と流束密度の計算問題を解いてみよう【演習問題】
- 流速と流束(フラックス)の違いは? 流束の種類
- レイノルズ数、ファニングの式とは?導出方法と計算方法【粘性力と慣性力の比】
- 単蒸留とは?レイリーの式の導出と単蒸留の図積分を用いた計算問題【演習問題】
- フラッシュ蒸留と単蒸留とフラッシュ蒸留の違いは?【演習問題】
- 連続蒸留とは?蒸留塔の設計における理論段数・最小還流比とは?【演習問題】
- 蒸留塔における理論段数の算出方法(McCabe-Thiele法による作図)は?理論段数・最小還流比とは?【演習問題】
- ベルヌーイの定理とは?ベルヌーイの定理の問題を解いてみよう【演習問題】
- 反応器(CSTRとPFR)の必要体積の比較の問題【反応工学の問題】
- 逐次反応 複合反応の導出と計算【反応工学】
- 並列反応 複合反応の導出と計算【反応工学】
- 転化率・反応率・選択率・収率 導出と計算方法は?【反応工学】
- 平均滞留時間 導出と計算方法【反応工学】
- 反応次数の計算方法 0次・1次・2次反応【反応工学】
- 含水率とは?湿量基準含水率と乾量基準含水率の違いは?
- 参考文献
- ヌッセルト数(ヌセルト数)・グラスホフ数・プラントル数
- レイリー数(レーレー数)とは?
- U字管マノメーターの原理と計算方法
- 層流・乱流・遷移領域とは?層流と乱流の違い
- 熱伝導率と熱伝達率の違い【熱伝導度や熱伝達係数との違い】
- フィックの法則の導出と計算【拡散係数と濃度勾配】
- 熱抵抗を熱伝導率から計算する方法【熱抵抗と熱伝導率の違い】
- 【ハ-ゲンポアズイユの定理】円管における層流の速度分布を計算する方法
- 質量保存則と一次元流れにおける連続の式 計算問題を解いてみよう【圧縮性流体と非圧縮性流体】
- 静圧と動圧の違い【位置エネルギーと運動エネルギー】
- ゲージ圧力と絶対圧力の違いは?変換(換算)の計算問題を解いてみよう【正圧と負圧の違いは?】
- 熱流束・熱フラックスを熱量、伝熱量、断面積から計算する方法【熱流束の求め方】