反応器(CSTRとPFR)の必要体積の比較の問題【反応工学の問題】
ここでは、反応工学の中でも反応器であるCSTR(連続槽)、PFR(管型押し出し流れ反応器)の種類と設計に関する以下の内容を解説していきます。
・CSTR(連続槽型反応器)における反応容器の体積の導出
・PFR(押し出し流れ反応器)における反応容器の体積の導出
・CSTRとPFRの反応器の体積の比較の問題を計算してみよう【演習問題】
というテーマで解説していきます。
CSTR(連続槽型反応器)における反応容器の体積の導出
反応工学における反応器設計の問題として、CSTR(連続槽型反応器)とPFR(管型反応器)の反応式がよくでてきます。
CSTRとPFRでは、ある化学反応において反応率Xが一定値になるために必要な反応器の体積が異なります。
以下で各々の装置で、必要な反応器の大きさの導出を行います。
まずは、CSTRにおける反応に必要な体積の導出を行っていきます。
CSTR(連続槽型反応器)における反応器容積を求めるためには、設計方程式が必要になります。
CSTRにおける設計方程式の導出は別途ページで記載しています。
設計方程式は以下のように定義されます。
体積流量とν0として、成分Aの初期濃度をCA0、反応率をxA、反応速度をrAとしたとき、rA V + CA0 ν0 xA = 0となります。
この計算式を変形し、V=の形にすると以下のようになります。V = (CA0 ν0 xA) / (-rA ) となります。この式は定容系の反応であっても、非定容系の反応であっても成り立ちます。

つまり、横軸に反応率xAをとり、縦軸に 1 / (-rA) をとった曲線を書いたときの下の面積が反応体積に相当します。
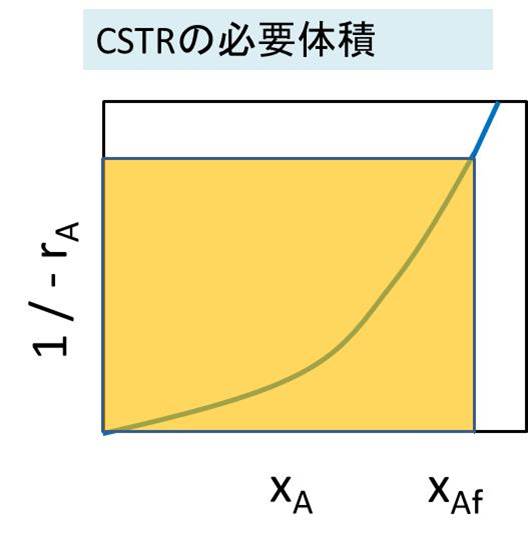
CSTRでは、長方形の面積を考えればいため、基本的に計算が簡単です。
関連記事
図積分
逐次反応の計算方法
転化率・反応率とは
平均滞留時間とは
定常状態近似 ミカエリスメンテン式とは
PFR(押し出し流れ反応器)における反応容器の体積の導出
PFR(押し出し流れ反応器)における反応器容積を求めるためには、設計方程式が必要になります。
PFRにおける設計方程式の導出は別途ページで記載しています。
設計方程式は以下のように定義されます。
体積流量とν0として、成分Aの初期濃度をCA0、反応率をxA、反応速度をrAとしたとき、rA + CA0 ν0 dxA / dV = 0となります。
この計算式を変形し、dV=の形にすると以下のようになります。dV = (CA0 ν0 dxA) / (-rA xA) となります。この式は定容系の反応であっても、非定容系の反応であっても成り立ちます。
そして、両辺を積分することで、必要体積Vの算出ができます。以下の通りです。
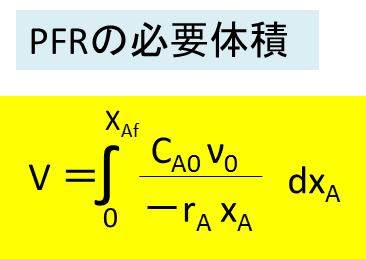
この計算式において、分子のCA0 ν0 はインテグラルの外に出すことができるため、実際に考慮すべきは、それ以外の以下の部分といえます。
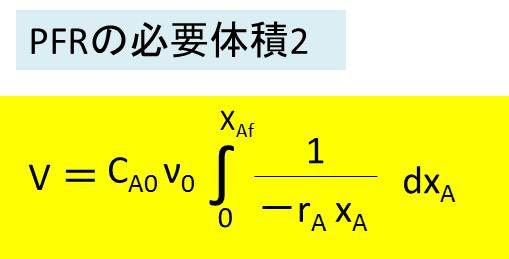
つまり、横軸に反応率xAをとり、縦軸に 1 / (-rA xA) をとった曲線を書いたときの下の面積が反応体積に相当します。
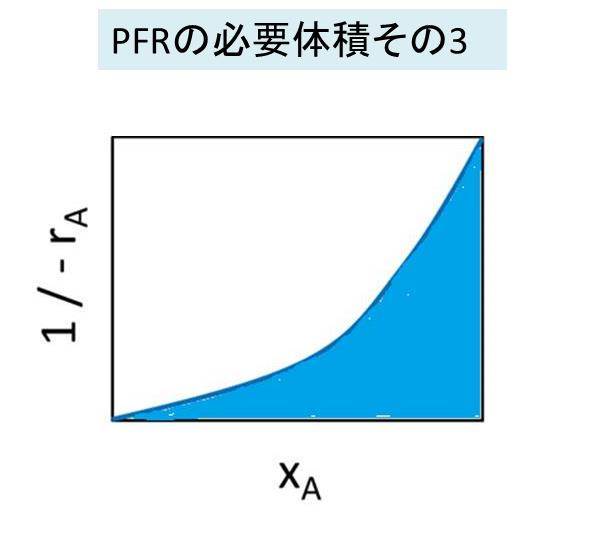
もし、曲線の詳細がわからないケースで、数点のプロットのみがデータとして得られるようなケースでは、図積分を用いて行うといいです。
関連記事
図積分
逐次反応の計算方法
転化率・反応率とは
平均滞留時間とは
定常状態近似 ミカエリスメンテン式とは
CSTRとPFRの反応器の体積の比較の考え方【演習問題】
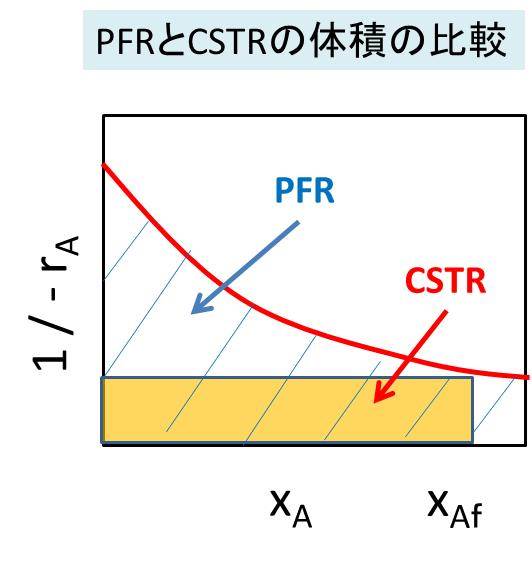
このように、CSTRとPFRでは、必要な反応器の体積の計算式が異なります。そして、その体積は先にものべた曲線の形によって、変化します。
上の例に述べた、曲線が単調に上昇していくケースでは、長方形よりも積分形の方が面積は小さく、PFRの方が有利とわかります。
一方で、以下のような単調減少の場合があったとします。すると、CSTRの方が面積が小さくて済みます。
つまり、反応体積がCSTRの方が小さくてよく、有利であるという比較・判断ができるのです。
関連記事
図積分
逐次反応の計算方法
転化率・反応率とは
平均滞留時間とは
定常状態近似 ミカエリスメンテン式とは
反応器(CSTRとPFR)の必要体積の比較の問題【反応工学の問題】 関連ページ
- 熱の伝わり方(伝熱の仕方)の種類
- フーリエの法則と熱伝導(伝導伝熱) 平板・円筒・球での熱伝導度(熱伝導率)の計算方法
- 多層平板における熱伝導(伝導伝熱)と伝熱抵抗 熱伝導度の合成
- ニュートン冷却の法則や総括伝熱係数(熱貫流率・熱通過率)とは?【対流伝熱】
- ニュートン粘性の法則の導出と計算方法 ニュートン流体と非ニュートン流体とは?【粘性係数(粘性率)と速度勾配】
- 放射伝熱(輻射伝熱)とは?プランクの法則・ウィーンの変位則・ステファンボルツマンの法則とは?
- 熱交換器の計算問題を解いてみよう 対数平均温度差(LMTD)とは?【演習問題】
- 比熱の測定方法(簡易版)
- 熱伝導率の測定・計算方法(定常法と非定常法)(簡易版)
- 熱拡散率(温度拡散率)と熱伝導率の変換・計算方法【演習問題】
- 反応速度と定常状態近似法、ミカエリス・メンテン式
- ラウールの法則とは?計算方法と導出 相対揮発度:比揮発度とは?【演習問題】
- 蒸気圧と蒸留 クラウジウス-クラペイロン式とアントワン式
- 流速と流量の計算・変換方法 質量流量と体積流量の違いは?【演習問題】
- 流束と流束密度の違いは? 流束と流束密度の計算問題を解いてみよう【演習問題】
- 流速と流束(フラックス)の違いは? 流束の種類
- レイノルズ数、ファニングの式とは?導出方法と計算方法【粘性力と慣性力の比】
- 単蒸留とは?レイリーの式の導出と単蒸留の図積分を用いた計算問題【演習問題】
- フラッシュ蒸留と単蒸留とフラッシュ蒸留の違いは?【演習問題】
- 連続蒸留とは?蒸留塔の設計における理論段数・最小還流比とは?【演習問題】
- 蒸留塔における理論段数の算出方法(McCabe-Thiele法による作図)は?理論段数・最小還流比とは?【演習問題】
- ベルヌーイの定理とは?ベルヌーイの定理の問題を解いてみよう【演習問題】
- 逐次反応 複合反応の導出と計算【反応工学】
- 並列反応 複合反応の導出と計算【反応工学】
- 転化率・反応率・選択率・収率 導出と計算方法は?【反応工学】
- 平均滞留時間 導出と計算方法【反応工学】
- 反応次数の計算方法 0次・1次・2次反応【反応工学】
- 粒子の沈降とは?ストークスの法則(式)と終末速度の計算方法【演習問題】
- 含水率とは?湿量基準含水率と乾量基準含水率の違いは?
- 参考文献
- ヌッセルト数(ヌセルト数)・グラスホフ数・プラントル数
- レイリー数(レーレー数)とは?
- U字管マノメーターの原理と計算方法
- 層流・乱流・遷移領域とは?層流と乱流の違い
- 熱伝導率と熱伝達率の違い【熱伝導度や熱伝達係数との違い】
- フィックの法則の導出と計算【拡散係数と濃度勾配】
- 熱抵抗を熱伝導率から計算する方法【熱抵抗と熱伝導率の違い】
- 【ハ-ゲンポアズイユの定理】円管における層流の速度分布を計算する方法
- 質量保存則と一次元流れにおける連続の式 計算問題を解いてみよう【圧縮性流体と非圧縮性流体】
- 静圧と動圧の違い【位置エネルギーと運動エネルギー】
- ゲージ圧力と絶対圧力の違いは?変換(換算)の計算問題を解いてみよう【正圧と負圧の違いは?】
- 熱流束・熱フラックスを熱量、伝熱量、断面積から計算する方法【熱流束の求め方】