χ2検定(ピアソンのχ2検定)
このページではピアソンのχ2値を用いたχ2検定について解説します。
通常のχ2値(こちらで解説しています)とピアソンのχ2値は厳密に言うと異なるため区別して考えます。
ピアソンのχ2値は各値自体から算出できるためノンパラメトリック手法の一部と考えられます。
(パラメトリック手法、ノンパラメトリック手法についてはこちら で解説しています)。
・適合度の検定(ピアソンのχ2検定とも呼ばれます)
・独立性の検定(こちらもピアソンのχ2検定と呼ばれます)
をこのページでは解説しています。
適合度の検定(ピアソンのχ2検定)
適合度の検定とは、χ2分布を用い実際のデータと理論値(期待値)とのズレを検定するものといえます。
(統計的検定の概要はこちらで解説しています)。
ピアソンのχ2値は下記式で表されます。

具体的には、母集団の理論値がわかっている場合(例えば5ケタの数字の組み合わせで宝くじを作った場合、当選くじにおいて各々の数字が出る確率は各々1/10であること等)、ある標本データが理論値に従っているかどうかを判断する際などに使用します。
下記データを元に実際に検定してみましょう。これは、上述しました5ケタの宝くじの当選くじ10枚における各数字の出現回数の結果です(架空のデータです))。各々の数字の出現回数は以下の通りであり、理論値は0~9の数字各々において1/10です(最も大きい位が0の場合も有りとします)。
ここで
・帰無仮説H0:実測値と理論値に差はない(つまり同じ)。
・対立仮説H1:実測値と理論値に差がある。
とします。
ピアソンのχ2値の式に基づき、計算を進めると以下のようになります。

すると、ピアソンのχ2値は17.2となります。
ここで有意水準5%として片側検定にかけるとしますと、χ2分布表(自由度は10-1で9となります)より限界値は16.92と読み取れます。(片側検定と両側検定の違いはこちらで解説しています。)
よって、有意水準5%の限界値を超えているため、帰無仮説が棄却され、理論値からズレている結果という判断ができます。
今回のデータはあえてズレが大きいデータを用いましたが、ズレが少なすぎる場合(理論値に近すぎる場合)もデータに何かしらの問題がある可能性が高くなります(ズレが少ない側を検定するには、両側検定もしくは片側検定(低い側)にかける必要があります。)
関連記事
パラメトリック手法、ノンパラメトリック手法の違いは?
独立性の検定(ピアソンのχ2検定)
独立性の検定とは、クロス集計表における行と列が関係しているかどうかを判断する検定のことです。
ピアソンのχ2値は適合度の検定においても記載した値を使用します。ただしこの場合の和はクロス集計表すべての値を足したものです。
2×2のクロス集計表を元に考えると理解しやすいため、下記データを用い考えていきましょう。
TV、PCの鑑賞時間5時間/日以上見る場合と見ない場合とで、視力矯正の有無(メガネやコンタクトの装着の有無)に影響を与えるかどうかの検定を行います。
ここで
・帰無仮説H0:TV、PCを5時間/日以上見るか見ないかは、視力矯正有無に影響しない。
・対立仮説H1:TV、PCを5時間/日以上見るか見ないかは、視力矯正有無に影響する。
とします。
下の表1つ目が実測値、下の表2つ目が期待値を表しています。また、期待値は帰無仮説をベースに考えます。よって、期待値はTV、PCを5時間/日以上見る見ないに関わらず、同数で視力矯正有り、無しが発生すると考えられるため、下の表の通りになります。
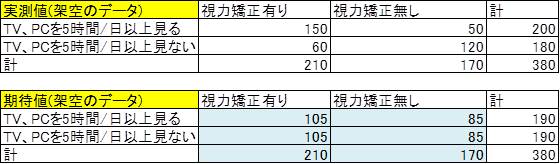
すると、ピアソンのχ2値=(150-105)2/105 + (85-50)2/85・・・と計算していき67.2となります。
ここで自由度は片方につき2水準ある中から基準の1水準を引き、掛け合わせるため
自由度=(2-1)×(2-1)=1となります。
ここで有意水準5%として片側検定にかけるとしますと、χ2分布表(自由度1)より限界値は3.841と読み取れるため、帰無仮説は棄却され、対立仮説TV、PCを5時間/日以上見るか見ないかは、視力矯正有無に影響するが採用されます(この架空データのケースでは)。
関連記事
パラメトリック手法、ノンパラメトリック手法の違いは?
また、当サイトのメインテーマであるリチウムイオン電池、電気化学関連の用語は以下でまとめています。
興味がある方は参考にしてみてください。
ピアソンのχ2検定(ノンパラメトリック手法) 適合度の検定、独立性の検定 関連ページ
- Excelデータ分析ツール使用の前準備
- 度数分布表とヒストグラム
- 【Excel】平均とは?(算術平均と加重平均) AVERAGEIF関数で条件付き(~以上かつ以下、~以上かつ未満、不等号、日付の範囲指定)の平均値を算出してみよう
- 【Excel】平均とは?2 (幾何平均、移動平均)
- 【Excel】分散と標準偏差:SDとは?基本統計量とは?Excel関数(VARP関数、STDEVP関数)で分散と標準偏差を計算してみよう
- 【Excel】変動係数(CV)とは?エクセルで計算してみよう【相対標準偏差:RSD】
- 標本と母集団
- 信頼区間の推定
- 信頼区間の推定をExcelを用いて行ってみよう!
- 【演習問題】信頼区間の推定を実際に行ってみよう CONFIDENSE.T関数とCONFIDENCE関数の違いは?【Excel】
- 二項分布
- 【Excel】正規分布とは?NORM.S.DIST関数で正規分布を描いてみよう【演習問題】
- 【Excel】ポアソン分布とは?POISSON関数、POISSON.DIST関数の使用方法【演習問題】
- 正規分布の応用技術(自動運転車におけるAI)
- 推測統計学とt分布
- χ2(カイ二乗)分布とは
- 【Excel】正規分布における歪度と尖度をSKEW関数、KURT関数で計算してみよう【演習問題】
- 【Excel】RAND関数、RANDBETWEEN関数を用いて乱数を作ってみよう 正規分布に従う乱数発生方法は?【演習問題】
- F分布
- 統計的検定の概要
- 2群の差の検定(t検定)と検定フロー
- F検定(等分散かどうかの検定)
- F検定(等分散かどうかの検定)を分析ツールを使用せずに行う方法
- Excel関数(FINV、F.INV.RT関数)でF検定時の上側確率に対応するF値を算出する方法
- Excel関数(TINV、T.INV.2RT関数)でt検定時の両側確率に対応するt値を算出する方法
- 等分散の時のt検定
- 等分散でない時のt検定(ウェルチの検定)
- パラメトリック手法とノンパラメトリック手法の違い ノンパラの紹介
- マン・ホイットニーのU検定
- 【Excel】マクネマー検定とは?Excelを使用して演習問題を解いてみよう!
- 【Excel】Wilcoxonの符号付順位和検定とは?Excelを使用して演習問題を解いてみよう!
- 【Excel】相関、相関係数とは?COOREL関数、PEASON関数、分析ツールで算出しよう【演習問題】
- 【Excel】共分散とは?COVAR関数,COVARIANCE.P関数を使用して共分散を求めてみよう COVARIANCE.P関数と.S関数の違いは?【演習問題】
- 【Excel】階乗の計算方法 FACT関数で階乗を求めてみよう【演習問題】
- 参考文献
- 【Excel】関数を使わずにデータを間引く方法【一定間隔の抽出】
- 【Excel】関数を使用してデータを間引く方法(INDIRECT関数)
- 【Excel】関数を使わずにn行ずつ空欄を追加する方法
- 【Excel】数字の間にハイフンを一括して入れる方法
- 【Excel】-(ハイフン)を入力した郵便番号の-を消す、再度つける方法
- 【Excel】Forecast関数で直線補間してみよう!Trend関数との違い
- 【Excel】SUMPRODUCT関数で積の合計を計算しよう!SUM関数との違い
- 【Excel】SUMIFS関数で複数条件の和の計算を行ってみよう!~以上かつ以下、~以上かつ未満、不等号、日付の範囲指定【演習問題】
- 【Excel】°(度)とrad(ラジアン)の変換方法【計算の考え方】
- 【Excel】勾配の計算方法 Excelを用いて勾配を計算してみよう
- 【Excel】sin曲線(サインカーブ)・cos曲線(コサインカーブ)を書く方法
- 【Excel】RMS(Root Mean Square:二乗平均平方根)と標準偏差の違いは?RMSの計算問題を解いてみよう【演習問題】
- 【Excel】工程能力指数のCP,CPK,PPKとは?片側規格と両側規格の違い CPKから不良率を算出する方法は?計算問題を解いてみよう【演習問題】
- 【Excel】Vlookup関数の使用方法
- 【Excel】STDEV関数(STDEV.S関数)とSTDEVP関数の違い
- 【Excel】VAR関数(VAR.S関数)とVARP関数の違い
- 【Excel】指定の倍数ごとに切り上げる方法 5ずつ切り上げる方法 1-5を5、6-10を10とする方法
- 【Excel】2つのif関数でデータを3種類に分類する方法 (A以上B以下)
- 【Excel】条件に合うデータの数量の数え上げ Countif,Countifs関数
- 【Excel】Excelソルバーで最適化問題を解こう!生産計画,線形計画問題【演習問題】
- 【Excel】Excelソルバーで最適化問題を解こう!二次関数の問題【演習問題】
- 【Excel】非表示列や行の再表示を一括で行う方法
- 【Excel】文の先頭に同じ文字を一括で追加する方法
- 対数の変換における2.303とは?常用対数と自然対数の変換
- 両側検定と片側検定の違い
- 分散分析 対応の無い場合の一元配置の分散分析をExcelで行ってみよう
- 分散分析 対応の有る場合の一元配置の分散分析をExcelで行ってみよう
- 分散分析 繰り返しの無い、有る場合の二元配置の分散分析をExcelで行ってみよう
- 多重比較法とは?分散分析との違い Tukeyの方法
- 数量化I類とは?Excelを用いて定性的なデータ(質的データ)の重回帰分析を行ってみよう
- 重回帰分析とは?Excel分析ツールで定量データの重回帰分析を行ってみよう!【リチウムイオン電池のデータ解析】
- 【Excel】最小二乗法とは?INTERCEPT関数とSLOPE関数の使用方法【単回帰分析、重回帰分析】
- 【Excelまとめ】Excel関数、分析ツールで統計解析を行おう
- 品質工学におけるFTA(故障の木解析)とは何か?FTAの原理とやり方
- 品質工学におけるFMEA(故障モード影響解析)とは何か?FMEAの原理とやり方
- 多変量解析 主成分分析と因子分析とは?違いは?
- 実験計画法
- 【Excel】Excelで対数関数の計算・グラフを書いてみよう!
- 【Excel】アークサインsin-1・アークコサインcos-1・アークタンジェントtan-1の計算方法【Excel】
- 材料証明書とミルシートの違い
- 【Excel】折れ線グラフで途中から点線にする方法
- 【Excel】折れ線グラフで途中の一部を消す方法
- 【Excel】折れ線グラフで途中から色を変える方法【色分け】
- 【Excel】数値の末尾に0を表示させ有効数字をそろえる方法
- 【Excel】円グラフで並び替えを行う方法【大きい順・小さい順】
- 【Excel】RANK関数を使用して数値の抽出・順位づけを行ってみよう
- 【Excel】エクセルを使用して割合や構成比を求める方法
- 【Excel】エクセルで文字を丸囲みする方法
- 【Excel】エクセルで必要ないスペースを一括で削除する方法
- 【Excel】エクセルで上付き文字と下付き文字を同時で行う方法
- 【Excel】エクセルでレ点(チェックマーク)を入力・編集・削除する方法
- 【Excel】「どっちが安いか」を計算する方法【値段の比較】
- 【Excel】前年比・伸び率・増減率(増加率・減少率)を計算する方法
- 【Excel】工場や施設の稼働率の定義と計算方法【演習問題】
- 【Excel】比率の計算方法(x:yに分ける方法)
- 【Excel】倍率の計算方法【入試の倍率・競争倍率】
- 【Excel】エクセルにおいて可視セルのみをコピーする方法
- 【Excel】途中で切れている折れ線グラフをつなげる方法【データ要素を線で結ぶ】
- 【Excel】利益と粗利の違い 利益率(粗利率)を計算する方法
- 【Excel】エクセルでセルに色を付けると枠線が消えるときの対処方法
- 【Excel】アスペクト(縦横比)を簡単に計算する方法 GCD(最大公約数)関数を使用しよう
- 【Excel】最大公約数を計算する方法 GCD関数の使用方法
- 【Excel】数字を絶対値を表示する方法 絶対値の最大値・最小値を求める方法
- 【Excel】エクセルのファイルにパスワードをかけ保護する方法・解除する方法
- 【Excel】最小公倍数を計算する方法 LCM関数の使用方法
- 【Excel】特定の文字を入力すると行の色が変わる設定方法【自動】
- 【Excel】エクセルで男女比を計算する方法
- 【Excel】エクセルで平均年齢を計算する方法 男女別の平均年齢を求める方法【誕生日から計算】
- 【Excel】エクセルで数値を丸める方法 四捨五入してみよう【ROUND関数】
- 【Excel】エクセルで勝手にで四捨五入されないようにする方法
- 【Excel】エクセルで小数点以下を切り捨てる方法 INT関数やTRUNC関数の使用方法
- 【Excel】エクセルでもともとある罫線を消す方法【薄い線の消し方】
- 【Excel】エクセルにおいて行と列のどっちがどっちかわからなくなったときの対処方法
- 【Excel】エクセルでファイルをpdf化する方法
- 【Excel】エクセルにおいて行と列の入れ替えを行う方法 Transepose関数の使用方法
- 【Excel】エクセルでBMIを求める方法
- 【Excel】エクセルで出席率・受講率・参加率を計算する方法
- 【Excel】エクセルで合格率・不合格率を計算する方法
- 【Excel】偏差平方和とは?計算問題を解いてみよう【演習問題】
- 【Excel】エクセルで達成率・進捗率を計算する方法
- 【Excel】エクセルで提出率を計算する方法
- 【Excel】エクセルで満点を変換する方法【120点を100点に換算】
- 【Excel】前月比・前日比・前週比を計算する方法
- 【Excel】人口密度を計算する方法
- 【Excel】エクセルで表示した近似曲線の式を出し、数式から値を求める方法
- 【Excel】エクセルで睡眠時間を計算する方法
- 【Excel】エクセルで残り時間・残日数・残月数を計算する方法
- 【Excel】エクセルで累積の計算をする方法
- 【Excel】エクセルで累積比率を計算する方法
- 【Excel】エクセルで表示した近似曲線の式の有効数字の桁数を変更する方法
- 【Excel】エクセルで表示した近似曲線の式に出るEの意味
- 【Excel】エクセルで表示した近似曲線を延長する方法【近似曲線の前方補外・後方補外】
- 【Excel】エクセルでロット数の計算・管理を行う方法【Celling関数】
- 【Excel】エクセルで基準値との差を計算する方法【プラスマイナス】
- 【Excel】エクセルのグラフに目標値などの基準線(目標線)を追加する方法【散布図と水平な平均線】
- 【Excel】エクセルで見え消し線・取り消し線を一部だけに引く方法
- 【Excel】エクセルで見え消し線・取り消し線を赤色などの色に変更する方法
- 【Excel】エクセルで見え消し線・取り消し線を二重線にする方法
- 【Excel】折れ線グラフに点を追加し、大きさ・色・形を変える方法
- 【Excel】エクセルでの割り算で商と余りを計算する方法【INT関数とMOD関数の使用方法】
- 【Excel】エクセルでの2行ごと・3行ごと・5行ごとなどまとめて合計する方法【一定間隔の合計】
- 【Excel】エクセルでexpの計算を行う方法 expのグラフを作成する方法
- 【Excel】エクセルでルート(平方根)の計算を行う方法 SQRTの使用方法
- 【Excel】エクセルで2乗、3乗などのn乗計算を行う方法 POWER関数の使用方法
- 【Excel】エクセルでミリ秒(ms)を計算する方法
- 【Excel】折れ線グラフに数値を一括で表示させる方法
- 【Excel】最後のn文字を一括で消す方法【後ろや右から消す】
- 【Excel】エクセルで勝手に日付に変換されるときの対処方法
- 【Excel】エクセルで最後の文字に一括で追加する方法
- サイコロを同時に振った場合の確率を求める問題のまとめ
- 【Excel】エクセルで最大値と二番目に大きい値を求める方法【LARGE関数の使用方法】
- 【Excel】エクセルで最小値と二番目に小さい値を求める方法【SMALL関数の使用方法】
- 【Excel】エクセルでセルの文字の中央揃えしてもずれる時の対処方法【中央揃えができない】
- 【Excel】エクセルで棒グラフと折れ線グラフを同時に表示し複合グラフを作る方法
- 【Excel】エクセルで棒グラフに区分線を引く方法【点線の追加】
- 【Excel】水槽などの水の容量の計算方法【リットルの計算】
- 【Excel】エクセルで3軸を表示する方法【散布図・折れ線グラフなど】
- 【Excel】エクセルで電流・電圧のグラフを作成する方法
- 【Excel】エクセルでsin・cos・tanを計算する方法【三角関数の計算】
- 【Excel】エクセルで税抜き・税込みの計算する方法【税抜き価格・税込価格】
- 【Excel】エクセルで片対数グラフを作成する方法(方対数ではない)
- 【Excel】エクセルで両対数グラフを作成する方法【両対数グラフの近似曲線の出し方】
- 【Excel】エクセルでlogやlnなどの対数の計算を行う方法【自然対数・常用対数の計算】
- 【Excel】エクセルで10の累乗(べき乗)を計算・表示する方法【指数計算】
- 【Excel】エクセルにて一括で頭に0をつける方法【電話番号・郵便番号など先頭に0を表示】
- 【Excel】エクセルにて一括で頭の0や00を消す方法【先頭の0を削除】
- 【Excel】エクセルでlogやlnを元に戻す方法【対数から真数へ】
- 【Excel】エクセルで「プラスだけ足す」「マイナスデータのみを抽出し合計する」方法
- 【Excel】エクセルで基準値以上の最小値を計算する方法【~以上という条件の最小値:DMIN関数】
- 【Excel】エクセルでルート(平方根)のグラフを作成する方法
- 【Excel】エクセルで2次関数(2次方程式)の計算を行う方法
- 【Excel】エクセルで2次関数(2次方程式)のグラフを作成する方法
- 【Excel】エクセルで全角と半角を変換する方法【カタカナ・数字など混在しているものの統一】
- 【Excel】文字が全角か半角かをチェック・判定する方法【LEN関数とLENB関数の組み合わせ】
- 【Excel】エクセルで累乗の分数(分数乗)を計算する方法(2/3乗など)
- 【Excel】三角形の角度を底辺や斜辺・高さから求める方法【直角三角形の角度の計算】
- 【Excel】三角形の斜辺の長さ・高さ・底辺の長さを残りの2辺からする方法【直角三角形の辺の求め方】
- 【Excel】エクセルで立方根(3乗根)を計算する方法(ルート3ではない】
- 【Excel】エクセルでルートや二乗を含んだ分数の計算を行う方法
- 【Excel】エクセルで左揃えでスペースを一括で追加する方法【左寄せ】
- 【Excel】エクセルで累乗根(1/n乗)を計算する方法【べき乗根】
- 【Excel】エクセルで今日の日付から「年だけ」「月だけ」「日だけ」や「月日のみ」「年月だけ」を抽出・表示する方法【TODAY関数・YEAR関数・MONTH関数・DAY関数】
- 【Excel】エクセルで達成率の平均を求める方法
- 【Excel】エクセルで階級値を計算する方法
- 【Excel】エクセルでsin2乗,cos2乗、tan2乗を計算する方法【sin^2,cos^2,tan^2】
- 【Excel】エクセルで中央値を求める方法 MEDIAN関数を使用してみよう【平均値と中央値】
- 【Excel】エクセルで出現回数のカウントをする方法・ランキングを作る方法【出現頻度の計算】
- 【Excel】エクセルで出現率の計算を行う方法
- 【Excel】エクセルを用いてアンケートの単一回答の集計を行う方法
- 【Excel】エクセルで連立一程式を解く方法 計算問題を解いてみよう【連立一次方程式】
- 【Excel】エクセルで標準誤差を計算する方法 標準誤差と標準偏差との違い
- 【Excel】エクセルで円の方程式から円のグラフを表示させる方法
- 【Excel】エクセルで行列の和や積の計算をする方法 スカラー倍の求め方【行列の掛け算・足し算】
- 【Excel】エクセルで逆行列の計算や転置行列を作る方法【MINVERSE関数の使用方法】
- 【Excel】エクセルで最頻値を求める方法 MODE関数・MODEMULT関数を使用してみよう【平均値と最頻値】
- 【Excel】エクセルで度数・相対度数・累積相対度数を計算する方法【FREQUENCY関数の使用方法】
- 【Excel】エクセルで一次関数を計算し、グラフを作る方法【一次関数の解を求める方法】
- 【Excel】エクセルで2点間の距離を計算する方法【2次元・3次元における2つの座標】
- 【Excel】エクセルで一定間隔の平均値を出す方法【行飛ばしの平均】
- 【Excel】エクセルでOFFSET関数を使用する方法【参照セルをずらす方法】
- 【Excel】エクセルで反比例のグラフや表を作成する方法
- 【Excel】エクセルで比例の関数やグラフを作成する方法【比例定数の計算】
- 【Excel】エクセルで勝率を計算する方法【勝率の出し方】
- 【Excel】エクセルで割引率(値引き率)や値引き後の価格を計算する方法【削減率の出し方】
- 【Excel】エクセルで絶対参照を相対参照に一括で変換する方法
- 【Excel】エクセルで四分位数(第一四分位数、第二四分位数、第三四分位数)を計算する方法
- 【Excel】四分位(ヒンジ)と四分位範囲、四分位偏差の計算方法【四分位数(ヒンジ)の求め方】
- 【Excel】エクセルで外れ値や異常値を判定する方法【四分位範囲(IQR)を用いた方法】
- サンプル数(標本サイズ)の決め方【サンプルサイズの計算方法】
- 【Excel】エクセルで行の高さや列の幅を一括で揃える方法【一括変更】
- 【Excel】エクセルで絶対値の平均を計算する方法
- 【Excel】エクセルでの双曲線のグラフの描き方【双曲線関数(sinh,cosh,tanh)】
- 【Excel】エクセルで質点の重心を求める方法【2質点の計算】
- 【Excel】エクセルで単位ベクトルを計算する方法【単位ベクトルの求め方】
- Excel】エクセルで余弦定理の計算をする方法【角度や辺の長さを求める】
- 【Excel】エクセルでベクトルの内積を計算する方法【内積の求め方】
- Excel】エクセルで正弦定理の計算をする方法【角度や辺の長さを求める】
- 【Excel】エクセルでベクトルの外積を計算する方法【外積の求め方】
- 【Excel】エクセルで同率の順位を表示させる方法【RANK関数で同順位にならないときの対処】
- 【Excel】エクセルで距離(位置)と時間から速度計算をする方法【速さの求め方】
- 【Excel】エクセルのオートフィル機能とは?オートフィル機能で一括処理をする方法
- 【Excel】エクセルでの正規化のやり方【最小値を0、最大値を1とする場合】
- 【Excel】エクセルで一定間隔で削除をする方法【1行ごと・n行ごとの削除】
- 【Excel】エクセルで一定間隔で挿入をする方法【1行ごと・n行ごとの挿入】
- 【Excel】エクセルで等差数列の和を計算する方法
- 【Excel】エクセルで等比数列の和を計算する方法
- 【Excel】エクセルでサイクロイドのグラフを書く方法【サイクロイド曲線】
- 【Excel】エクセルで楕円の式の計算やグラフを書く方法【楕円の方程式】
- 【Excel】エクセルで昨日・明日・明後日の日付を表示させる方法【Today関数の使用方法】
- 【Excel】エクセルでカージオイド(外サイクロイド)のグラフを書く方法【カージオイド曲線】
- 【Excel】エクセルで正葉曲線(バラ曲線)のグラフを書く方法【正葉曲線(バラ曲線)】
- 【Excel】エクセルで出勤率の計算を行う方法
- 【Excel】エクセルで10段階の相対評価を行う方法【PERCENTRANK.INC関数の使用方法】
- 【Excel】エクセルで五捨六入や六捨七入を行う方法
- 【Excel】エクセルでヘロンの公式により三角形の面積を求める方法【計算】
- 【Excel】エクセルでセル内に縦の線(罫線)を入れる方法【中心線の追加】
- 【Excel】エクセルで5段階評価を行う方法【PERCENTRANK.INC関数の使用方法】
- 【Excel】エクセルで円の面積から直径を計算したり、直径から面積を求める方法【PI関数の使用方法】
- 【Excel】エクセルで3段階評価を行う方法【ABC評価】
- 【Excel】エクセルで楕円の面積を計算する方法
- 【Excel】エクセルでインチとピクセルの変換を行う方法
- 【Excel】エクセルで一定の数値以上、以下の個数をカウントを出す方法【指定の数字より大きい、小さいものを数える】
- 【Excel】エクセルで一定の数値以上、以下の合計を出す方法
- 【Excel】エクセルで一定以上、以下の数値の色を付ける方法【指定値よりも大きい、小さい(未満)のセルの色分け】
- 【Excel】エクセルで上位Xパーセント(%)以上をA評価と判定する方法
- 【Excel】エクセルで月ごとの合計を出す方法【月毎の小計】
- 【Excel】エクセルで年ごとの合計を出す方法【年毎の集計】
- 【Excel】エクセルで日ごとの合計を出す方法【日毎の集計】
- 【Excel】エクセルでランキングの上位3位の合計を出す方法【上位10位や上位5位の計算も】
- 【Excel】エクセルで上位の数値を抽出する方法【上位3位や上位10位までの抽出も】
- 【Excel】エクセルで10進数と2進数の変換を行う方法【2進法と10進法】
- 【Excel】エクセルで入力するとセルの色が自動で変わるようにす方法
- 【Excel】エクセルで入力すると行の色が自動で変わるようにする方法
- 【Excel】エクセルで偏差値を計算する方法【偏差値の出し方】
- 【Excel】エクセルで指定した期間の平均を計算する方法
- 【Excel】エクセルで対角線の長さを計算する方法【長方形】
- 【Excel】エクセルで偶数や奇数の数をカウントする方法
- 【Excel】エクセルで偶数や奇数のセルに色付けを行う方法
- 【Excel】エクセルで平均以上のセルに色付けを行う方法【平均値以下も】
- 【Excel】エクセルで平均以上の数値をカウントする方法【平均値以下を数える】
- 【Excel】エクセルで温度と湿度のグラフを作成する方法
- 【Excel】エクセルで1時間当たりの生産量を計算する方法【生産性計算】
- 【Excel】エクセルでn行ごとに色を変える方法
- 【Excel】エクセルで濃度の計算をする方法
- 【Excel】エクセルで順列と組み合わせの計算を行う方法【場合の数】
- パーセントとパーセンタイルの違い
- MTBF(平均故障間隔)とMTTR(平均修理時間)の計算
- 【Excel】エクセルで1か月後、1か月前の日付を表示する方法【1か月足す、1か月引く】
- 【Excel】エクセルで期待値(期待度数)を計算する方法【サイコロやくじの期待値】
- 度分秒と度の変換(換算)方法【角度の単位の計算】
- 【Excel】エクセルで月ごとの平均を出す方法【月毎の平均】
- 【Excel】エクセルで時間の足し算を行う方法【1時間足す】
- 【Excel】エクセルで時間の引き算を行う方法【1時間引く】
- 【Excel】エクセルで足し算を飛び飛びに行う方法【1つ飛ばし】
- 【Excel】エクセルで足し算を一気に行う方法【一括で連続データを足す】
- 【Excel】エクセルでボタンを用いて指定したセルに移動させる方法【ハイパーリンク関数やマクロ(VBA)】
- sinθ=1を満たす角度は何度?sinθ=-1を満たす角度は何度か?