【ハ-ゲンポアズイユの定理】円管における層流の速度分布を計算する方法
ここでは化学工学の中でも、流体に関する考え方である「ハーゲンポアズイユの定理を用いて円管内の層流の速度分布を計算する方法」について解説していきます。
・ハーゲンポアズイユの定理を用いて円管内の層流の速度分布の導出・計算する方法
・速度分布の計算のために初期条件、境界条件を考える
というテーマで解説していきます。
ハーゲンポアズイユの定理を用いて円管内の層流の速度分布の導出・計算する方法
流体力学の基礎の考え方として重要なものに、円管内を流れる流体が層流である場合の速度分布が挙げられます。
層流とはこちらでも詳しく解説していますが、流体の流れが比較的穏やかである場合に規則正しい流体の流れとなります。この状態を層流と呼び、規則性があるために速度分布を計算できるのです。
ここでは、円管内の層流の速度分布を導出していきましょう。
以下のよう、ある円管内を流れる流体(ニュートン流体)の一部を抜き出して考えていきます。この速度分布を導出していくための、一部のモデルのことを検査体積と呼びます。
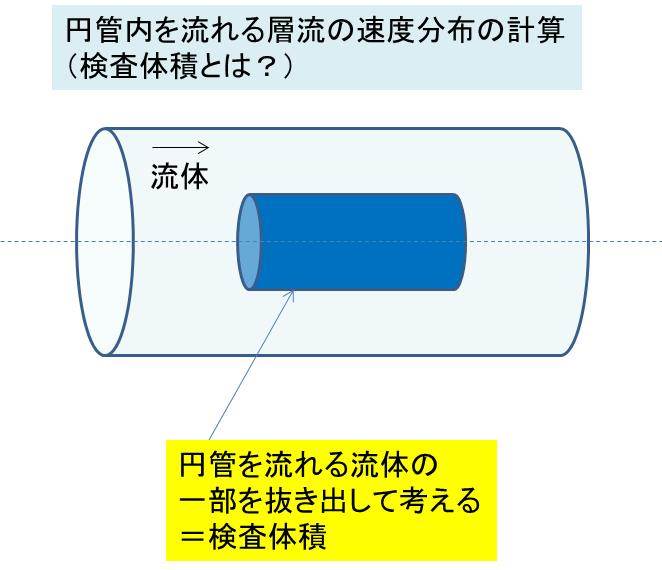
この検査体積にかかる力には、流体の入り口と出口の圧力の差の分の力と、流体にかかるせん断力があります。
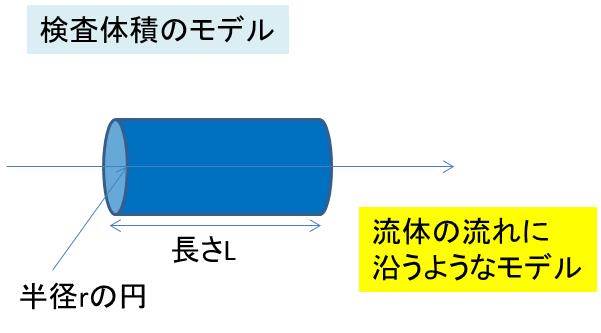
つまり、これらの力全体を考慮して、検査体積にかかる力の釣り合いを考えるといいのです。ここで、検査体積としては、管の形と併せて円筒形で考えるのが基本です。
なお、検査体積の具体的なサイズは半径r、長さLの円筒モデルとします。
このとき、入口の圧力をP入、出口の圧力をP出とし、せん断応力をτとし力の釣り合いを考えます。
すると、円の面積πr^2 × P入 =円の面積πr^2 × P出 + 円の側面積 2πrL × せん断応力τ という力の釣り合いの式が成立します。
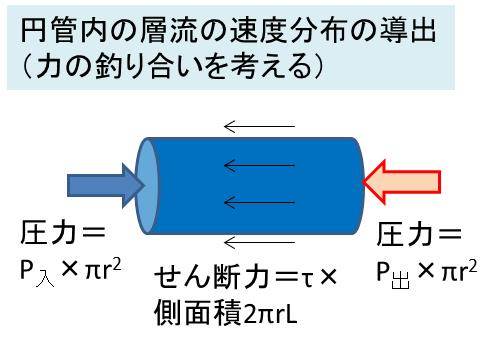
ここで、圧力差P入 - P出=⊿Pとおくと、 πr^2⊿P=2πrL × τ ・・・①となります。
さらに、ニュートン流体を仮定しているためにニュートン粘性の法則が適用できます。

ここで、円管であるため、上式yにはrが適用されることを考慮しますと、 ここでニュートン粘性の法則では正の向きによって符号が+の場合と-の場合があり、今回の場合は円管の出口から入口に向かう力となるため、-の符号をつけた「τ = - µ du/dr 」を採用します。
上の①式に代入しますと、 πr^2⊿P=2πrL × τ ⇔ πr^2⊿P=2πrL × (-µ du / dr)となります。
これを整理していくと、 r⊿P = -2Lµ × du/drとなります。
さらに変形させ、積分しやすい形にすると、 r dr = - 2Lµ / ⊿P du となります。
ここで両辺を0から任意のrまで積分すると、 r^2 /2 = - 2Lµ / ⊿P (u + C)⇔ (u + C) = - ⊿P / 4Lµ r^2 となるわけです。

ここまで、円管内の速度分布の導出のための式変形ができました。
最後の詰めをしていきます。
関連記事
層流と乱流とは?
ニュートン粘性の法則とニュートン流体
レイノルズ数(Re)やファニングの式とは?
速度分布の計算のために初期条件、境界条件を考える
後は、上の式の定数項を確定させるために、境界条件を考えていきます。
実際の円管の半径がRであるとすると、管壁(r=R)では速度uが0となります。この境界条件を上式に組み込んでいきましょう。
すると、C=- ⊿P / 4Lµ R^2 となります。
よって、u = ⊿P / 4Lµ (R^2 - r^2)= ⊿PR^2 / 4Lµ (1 - (r/R)^2)となるのです。

なお、r=0のとく最大流速となり、umax=⊿PR^2 / 4Lµ となります。
速度分布の導出は基本的に力の釣り合いと式変形のみで処理できるので、きちんと理解しておきましょう。
関連記事
層流と乱流とは?
ニュートン粘性の法則とニュートン流体
レイノルズ数(Re)やファニングの式とは?
【ハ-ゲンポアズイユの定理】円管における層流の速度分布を計算する方法 関連ページ
- 熱の伝わり方(伝熱の仕方)の種類
- フーリエの法則と熱伝導(伝導伝熱) 平板・円筒・球での熱伝導度(熱伝導率)の計算方法
- 多層平板における熱伝導(伝導伝熱)と伝熱抵抗 熱伝導度の合成
- ニュートン冷却の法則や総括伝熱係数(熱貫流率・熱通過率)とは?【対流伝熱】
- ニュートン粘性の法則の導出と計算方法 ニュートン流体と非ニュートン流体とは?【粘性係数(粘性率)と速度勾配】
- 放射伝熱(輻射伝熱)とは?プランクの法則・ウィーンの変位則・ステファンボルツマンの法則とは?
- 熱交換器の計算問題を解いてみよう 対数平均温度差(LMTD)とは?【演習問題】
- 比熱の測定方法(簡易版)
- 熱伝導率の測定・計算方法(定常法と非定常法)(簡易版)
- 熱拡散率(温度拡散率)と熱伝導率の変換・計算方法【演習問題】
- 反応速度と定常状態近似法、ミカエリス・メンテン式
- ラウールの法則とは?計算方法と導出 相対揮発度:比揮発度とは?【演習問題】
- 蒸気圧と蒸留 クラウジウス-クラペイロン式とアントワン式
- 流速と流量の計算・変換方法 質量流量と体積流量の違いは?【演習問題】
- 流束と流束密度の違いは? 流束と流束密度の計算問題を解いてみよう【演習問題】
- 流速と流束(フラックス)の違いは? 流束の種類
- レイノルズ数、ファニングの式とは?導出方法と計算方法【粘性力と慣性力の比】
- 単蒸留とは?レイリーの式の導出と単蒸留の図積分を用いた計算問題【演習問題】
- フラッシュ蒸留と単蒸留とフラッシュ蒸留の違いは?【演習問題】
- 連続蒸留とは?蒸留塔の設計における理論段数・最小還流比とは?【演習問題】
- 蒸留塔における理論段数の算出方法(McCabe-Thiele法による作図)は?理論段数・最小還流比とは?【演習問題】
- ベルヌーイの定理とは?ベルヌーイの定理の問題を解いてみよう【演習問題】
- 反応器(CSTRとPFR)の必要体積の比較の問題【反応工学の問題】
- 逐次反応 複合反応の導出と計算【反応工学】
- 並列反応 複合反応の導出と計算【反応工学】
- 転化率・反応率・選択率・収率 導出と計算方法は?【反応工学】
- 平均滞留時間 導出と計算方法【反応工学】
- 反応次数の計算方法 0次・1次・2次反応【反応工学】
- 粒子の沈降とは?ストークスの法則(式)と終末速度の計算方法【演習問題】
- 含水率とは?湿量基準含水率と乾量基準含水率の違いは?
- 参考文献
- ヌッセルト数(ヌセルト数)・グラスホフ数・プラントル数
- レイリー数(レーレー数)とは?
- U字管マノメーターの原理と計算方法
- 層流・乱流・遷移領域とは?層流と乱流の違い
- 熱伝導率と熱伝達率の違い【熱伝導度や熱伝達係数との違い】
- フィックの法則の導出と計算【拡散係数と濃度勾配】
- 熱抵抗を熱伝導率から計算する方法【熱抵抗と熱伝導率の違い】
- 質量保存則と一次元流れにおける連続の式 計算問題を解いてみよう【圧縮性流体と非圧縮性流体】
- 静圧と動圧の違い【位置エネルギーと運動エネルギー】
- ゲージ圧力と絶対圧力の違いは?変換(換算)の計算問題を解いてみよう【正圧と負圧の違いは?】
- 熱流束・熱フラックスを熱量、伝熱量、断面積から計算する方法【熱流束の求め方】