コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
こちらのページでは高校物理における電磁気学の中でも、並列時のコンデンサーの合成に関する内容について解説していきます。
・コンデンサーの並列回路における容量の求め方と導出方法 合成容量の計算
・コンデンサーを並列にした場合の合成容量の計算問題を解いてみよう
・コンデンサーは並列接続すると容量が大きくなる この理由は?
にというテーマで解説しています。
コンデンサーの並列回路における容量の求め方と導出方法 合成容量の計算
結論から言いますと、コンデンサーの並列つなぎにおける合成容量は、C合成 = C1 + C2という計算式が成り立ちます。

この結果を導くための過程を以下で確認していきます。
以下のように、電圧Vの起電力がある直流電源と並列に配置された二つのコンデンサーを含む回路があるとします。
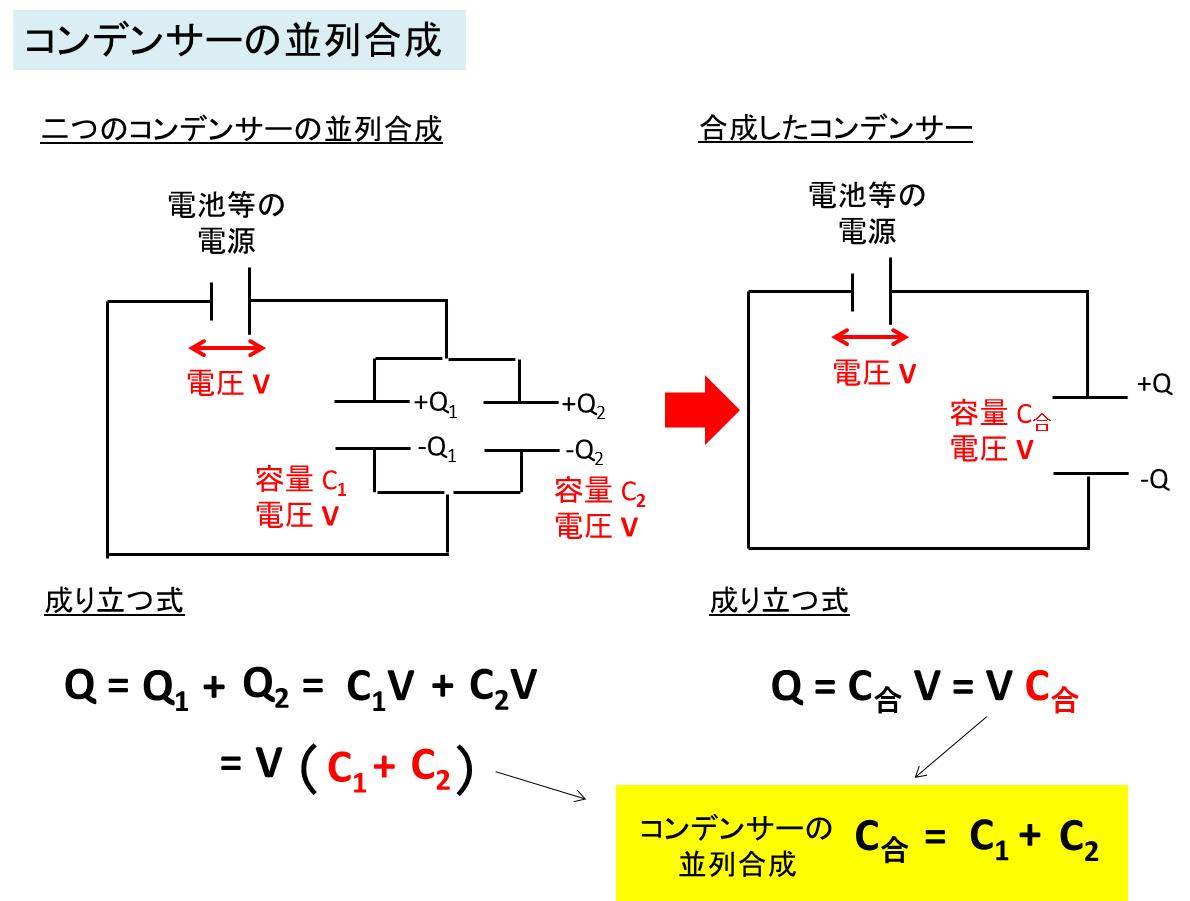
すると、電源のプラスにつないである各々の電極にはプラスの電荷が集まります。一方で、直流電源のマイナスに接続してある二つの電極には、マイナス(負)の電荷が溜められます。
並列接続であるために、コンデンサーに印加される電圧は同じですが、各々に溜められている電荷の量は、コンデンサーの静電容量に応じて異なります。
ここで、左からコンデンサーの記号をC1、C2とし、電圧をV(=V1=V2)とします。さらに、各々の極板にたまっている電荷の大きさをそれぞれQ1、Q2としましょう。
すると、静電容量と電圧、電荷の計算式からQ1=C1Vとなり、もう一方ではQ2=C2Vとなります。
全体の電荷をQとするとQ=Q1+Q2と記載でき、並列つなぎにおけるコンデンサーの合成容量をC合成とすると、Q=C合成 Vと表現できます。
このときに、C合成V=(C1 + C2) とであるため、C合成=C1+C2となるのです。
改めてこの計算式を記載しておきます。

このように、並列つなぎにおける合成容量が算出できることを理解しておきましょう。
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーとは?コンデンサーの静電容量の式と導出方法
コンデンサーの直列合成
ファラド、クーロン、ボルトの変換方法
コンデンサーを並列にした場合の合成容量の計算問題を解いてみよう
それでは、理解を深めるためにも、コンデンサーの並列接続における静電容量の合成の問題を解いてみましょう。
例題1
コンデンサー1の容量が4μF、もう一方のコンデンサー2の静電容量が6μFであるときに、直列に合成したコンデンサーの合成容量を計算してみましょう。
解答1
上でも解説したように、コンデンサーの並列回路では、単純和をとることで静電容量の合成ができます。
よって、C合成= 4 +6 = 10 より、コンデンサーの並列つなぎにおける静電容量(キャパシティ)は10μFとなるのです。
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーとは?コンデンサーの静電容量の式と導出方法
コンデンサーの直列合成
ファラド、クーロン、ボルトの変換方法
コンデンサーは並列接続すると容量が大きくなる この理由は?
このように、コンデンサーの並列回路における容量は、並列数が増えるほど増加します。
この直列時に静電容量が大きくなるメカニズム(仕組み)はコンデンサーの容量と電極面積との関係から理解できます。
静電容量と極板面積には以下の関係があります。
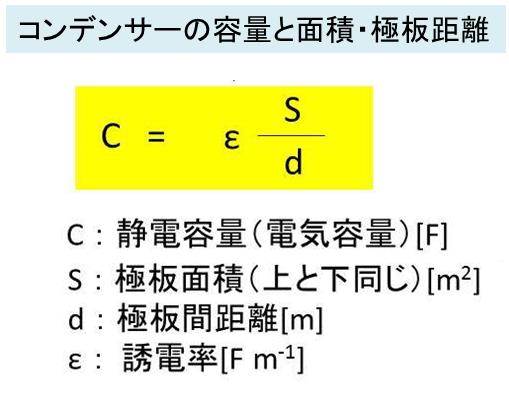
ここで、並列に合成した場合では、単純に一つの板の反応面積が大きくなったときと同じことになることが理由です。
つまり、各々の電極間の幅がS1,S2であったとすると、その表面積はS1+S2となります。
このコンデンサーの静電容量の極板面積は、比例の関係にあるため、並列つなぎでは、その容量が上昇するのです。
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーとは?コンデンサーの静電容量の式と導出方法
コンデンサーの直列合成
ファラド、クーロン、ボルトの変換方法
コンデンサーを並列接続したときの静電容量の計算方法【演習問題】 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】