距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
物理の問題が解けるようになるには、基礎の部分をきちんと理解しておくことが大事です。
中でも力学における基礎的な内容として、「距離、速度、加速度」という用語があり、これらを覚えておく必要があります。
ここでは、この距離、速度、加速度の定義や覚え方、各々の換算方法について解説していきます。
・距離・位置・変位とは?単位は?
・速度とは?速度は変異を微分したもので、変異は速度を積分したもの
・加速度とは?加速度は速度を微分したもので、速さは加速度を積分したもの
・変位・位置・距離と速度の変換の計算問題を解いてみよう
・速度と加速度の変換の計算問題を解いてみよう
というテーマで解説していきます。
距離・位置・変位とは?単位は?
位置とは、ある一次元(直線)において、基準を0としたときのある地点での値を指します。そして、ある位置と別の位置の差を変位や距離と呼びます。
以下のようなイメージです。
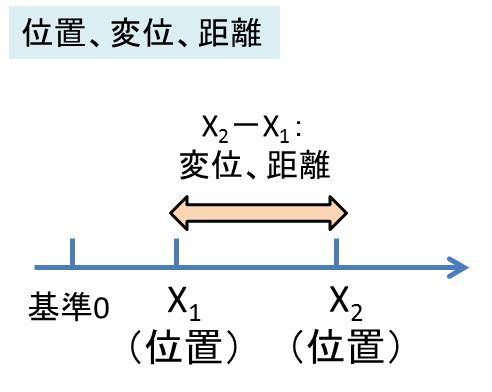
単位としては、長さの単位であるm、mm、cmなどを使用することが基本です。
関連記事
秒速m/sと時速km/hの変換方法
速度とは?速度は変異を微分したもので、変異は速度を積分したもの
一方で、速度とは、ある物体に着目したときに、一定時間に移動した距離をかかった時間で割ったものです。別の言い方では、速さともいいます。
以下のような計算式で表されます。

よって、速さの単位はm/sとなることが基本です(秒速m/sではなく時速km/hで表すこともあります)。
厳密な意味でのある位置x1における速度とは、ある時刻t1における位置をx1とし、別の時刻t2における位置をx2としたときのv(t1) = (x2(t2) - x1(t1)) / (t2 - t1) において、t2をt1まで近づけるように極限をとったものです。
以下のような式になります。

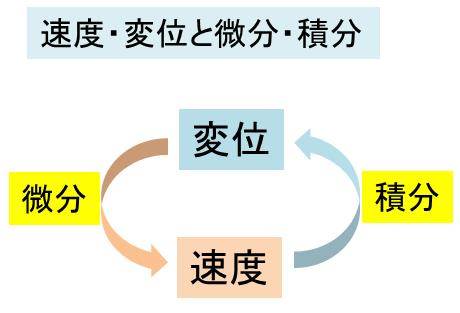
これは実は、微分の定義そのものであり、変位を微分したものが速度になるのです。よって、速度を積分したものが変位となるのです。
関連記事
秒速m/sと時速km/hの変換方法
加速度とは?加速度は速度を微分したもので、速さは加速度を積分したもの
加速度とは、ある物体に着目したときに、一定時間に変化した速度を変化した時間で割ったものです。
以下のような計算式で表されます。

加速度の単位はm/s^2となります。
厳密な意味でのある位置x1(時刻t1)における加速度とは、x1における速度をv1とし、別の位置x2(時刻t2)における速度をv2としたときのa(t1) = (v2(t2) - v1(t1)) / (t2 - t1) において、t2をt1まで近づけるように極限をとったものです。
以下のような式になります。

先ほどと同様にこれは、微分の定義そのものです。つまり、速度を微分したものが加速度になり、加速度を積分したものが速度となるのです。
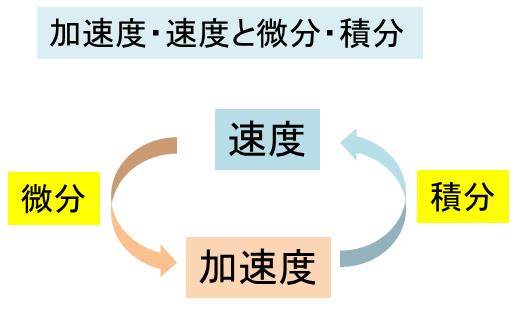
速度と距離の関係と、加速度と速度の関係は同じようなものといえます。
関連記事
秒速m/sと時速km/hの変換方法
変位・位置・距離と速度の変換の計算問題を解いてみよう
それでは、理解を深めるにも実際に問題を解いていきましょう。
例題1
時間0sのときにx=0の位置にいた球があるとします。この球は、5秒後にはx=8mの位置にいました。
速度一定である場合の、球の速度を求めてみましょう。
解答1
速度の公式従いましょう。 (8-0) / 5 =1.6 m/sの速さであることがわかります。
それでは、逆に速さから移動した距離を求める問題も解いてみましょう。
例題2
時間0sのときにx=3mの位置にいた球があるとします。この球はが4m/sという一定の速さで正の方向に進んでいるとします。このときの2s後の位置はいくつになるでしょうか。
解答2
元の位置がx=3mの位置にくることに気を付けましょう。よって、3 + 4 × 2 = 11mの位置にいることがわかります。
関連記事
秒速m/sと時速km/hの変換方法
速度と加速度の変換の計算問題を解いてみよう
同様に、速度と加速度の換算も行っていきましょう。
例題1
ある物体が、時間0sのときに5m/sの速度で移動していたとします。そして、8s後に速度9m/sの速度となっている場合の、加速度を計算していきましょう。
ただ、加速度は一定であるときを考えていきます。
解答1
加速度の定義に従いましょう。(9-5) / 8 =0.5 m/s^2の加速度であることがわかります。単位が普段見慣れないm/s^2であることに注意しましょう。
逆に加速度から速度の変化分を求める問題も解いてみましょう。
例題2
時間0sのときに速度1m/sで動いている物体があるとします。この物体が7m/s2という一定の加速度で速度を上げているとします。このときの2s後の速さはいくつになるでしょうか。
解答2
1 + 7×2 = 15m/sの速度と計算できるのです
一つ一つの定義をきちんと理解し、変異、速度、加速度の扱いに慣れていきましょう。
関連記事
秒速m/sと時速km/hの変換方法
距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】