単振動における変位・速度・加速度を表す公式と計算方法【sin・cosとの関係】
高校物理における力学の分野では、単振動に関する問題は良く出てきます。
ここでは、単振動の中でもsinやcos、角振動数ωなどを利用して作られる単振動の変位、速度、加速度の公式や計算方法について解説していきます。
・単振動とばねの復元力の公式(F=-kx)
・速度の最大や加速度の最大値・最小値(0)と変位の関係
・単振動の変位、速度、加速度の公式 sin・cosとの関係性は?【等速円運動との関係】
というテーマで解説していきます。
単振動とばねの復元力の公式(F=-kx)
単振動とは、ばねのように伸びたら縮もうとし、縮んだら伸びようとする現象のことを指します。単振動では、元の安定な状態に戻ろうとする力(復元力)を利用しています。
例えば、下図のように壁にばねがついており、摩擦のない土台の上に設置されているとします。ここで、ばねを引っ張り(もしきは縮める)、離すと単振動が開始されます。
単振動においてばねが自然長(変位x=0とする)のときは、復元力は働かず0です。一方でばねが伸びているときには、ばねの伸びxと力Fの公式からF=-kxという復元力が働くのです(kはばね定数)
同様にばねが縮むと、今度はばねを伸ばそうとする方向に復元力が働くのです。
以下のようなイメージです。
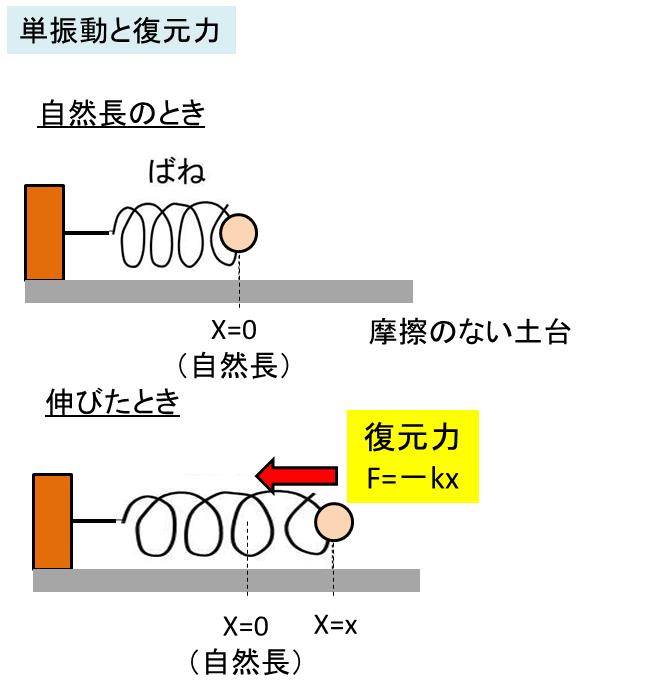
なお、このとき伸びる方向を正の値としてしているため、復元力はF=-kxと頭に負号がつくことに注意しましょう。
関連記事
ばね定数とは?ばね定数の合成方法
速度の最大や加速度の最大値・最小値(0)と変位の関係
また、単振動の問題として速度や加速度がどの位置で最大、最小となるのかが良く問われます。
これは、後程解説する単振動における位置、速度、加速度との計算式をみればわかります。ただ、直感的にイメージしておくも大事であり、以下で確認します。
上述のよう、単振動は「ばねを伸ばすか、圧縮するか」で始まり、このときの自然長からの距離をAとすると、変位の最大値はAとなり、逆に最小値は-Aとなるのです。
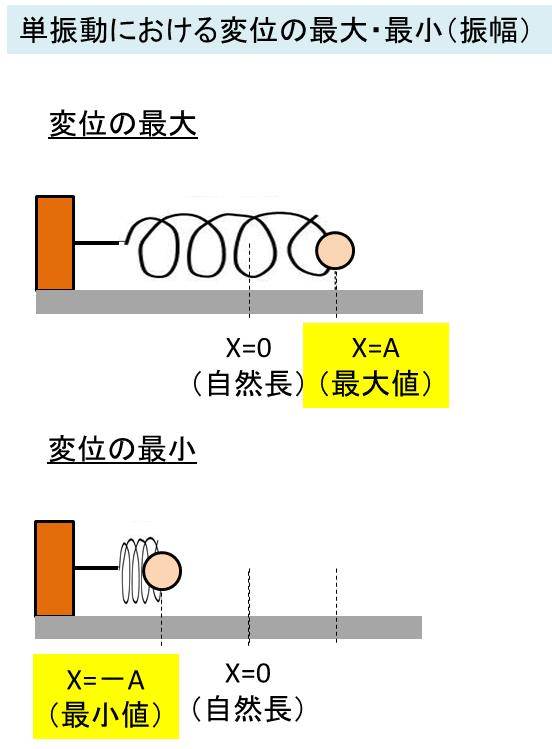
このように、単振動の変位が最大・最小となるときには、速度は0となります。この地点を元に、ばねが移動する向きが変わることを覚えておけば、この仕組みが理解しやすくなります。
そして、x=0と自然長となるときに、速度は最大となるのです。
一方で、変位が最大・最小、速度は0とのときには、加速度の大きさは最大となります。これは、復元力F=-kxの大きさが最大になることと絡めて理解しておくと覚えやすいです。
さらに、x=0のときは、今度は加速度も0となるのです。
このイメージと合わせて、単振動の変位、速度、加速度の公式を覚えておきましょう。結局のところ、sin関数、cos関数で表現することができるために、各々の値の最大、最小の関係が結び付けられるのです。
関連記事
位置、速度、加速度の変換方法は?
等速円運動における角速度の計算方法
単振動における運動方程式と角速度と周期の関係
単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
単振り子(振り子の単振動)における運度方程式や周期の計算
単振動の変位、速度、加速度の公式 sin・cosとの関係性は?【等速円運動との関係】
単振動の変位、速度、加速度の公式はsin(サイン)、cos(コサイン)、角振動数ω(等速円運動における角速度)、時間などを用いて以下のように表されます。

実は単振動では、等速円運動を直線上に投影したような動きをとります。
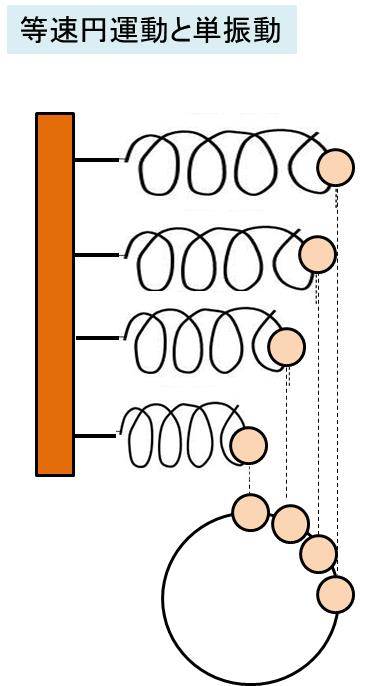
なお、変位の位置は等速円運動におけるsinの値を投影したものと一致するために、x=Asin(ωt)と表現できるのです。このときに、Aは振幅とよび、単振動における最大・最小の絶対値にあたります。
以下のようなイメージです。
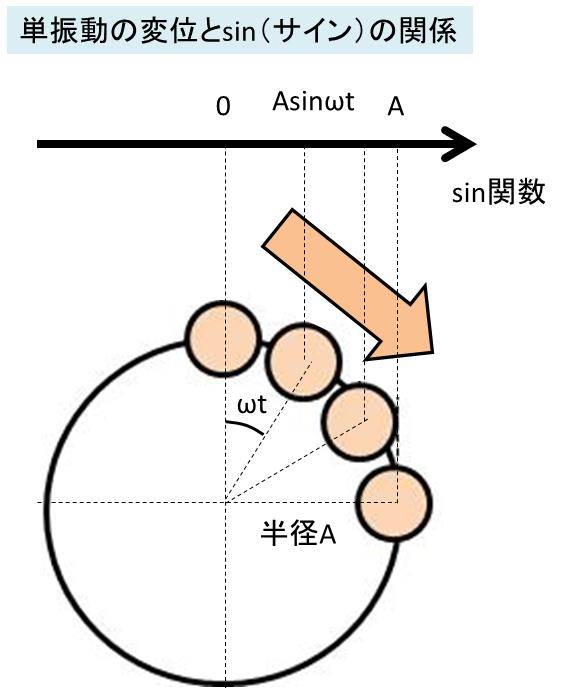
そして、「位置、速度、加速度の変換方法」でも解説していますが、単振動において変位がAsinωtとわかりましたら、速度はこの数式を微分するといいです。
Asinωtの時間tでの微分では、まずsinがcosにかわり、sinの中身のwtをtで微分したものが頭の係数にかかります。
よって Aω cos ωtが単振動における、速度と時間の関係式となるのです。
さらに、加速度は、速度を微分したものであるために、 Aω cos ωtにおいて、cosを-sinに変えた上で、ωtを微分したものであるωをさらに頭の係数にかけましょう。結果として、単振動における加速度は、 -Aω^2 sin ωtという計算式になるわけです。
なお、変位をxとし、加速度をaと表記しますと、 x = Asinωt から、加速度a = -Aω^2 sin ωt = -A ω^2 xと記載できます。この関係式は単振動における運動方程式から、角速度と周期を求める問題に利用するため、きちんと理解しておきましょう。

関連記事
位置、速度、加速度の変換方法は?
等速円運動における角速度の計算方法
単振動における運動方程式と角速度と周期の関係
単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
単振り子(振り子の単振動)における運度方程式や周期の計算
単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】