ロケットなどで2物体が分裂・合体する際の速度の計算方法【運動慮保存と相対速度】
物理における力学の分野ではよく、運動量保存則を適用して現象を解析することがあります。
たとえば、ロケットなどにおいて2つの物体が分解・合体する際の速度を計算する問題などが挙げられます。この2つの物体が分裂したり、衝突したりするときの前後の速度を求める方法について理解していますか。
ここでは、運動量保存則や相対速度の考え方を使用して、2つの物質が分解・合体する現象の解き方について解説していきます。
・ロケットの分裂に関する速度を計算してみよう【運動量保存則と相対速度】
・2物体が合体する際の計算問題を解いてみよう【片方が静止時の衝突の問題】
・両方が移動しているときの2物体が合体する際の計算問題を解いてみよう
というテーマで解説していきます。
ロケットの分裂に関する速度を計算してみよう【運動量保存則と相対速度】
ロケットなどの物体が分解する際の分裂後の速度を求める問題では、基本的に運動量保存則と相対速度の考え方を使用して計算できます。ほぼパターン問題といえるため、きちんと理解しておきましょう。
小型ロケットと大型ロケットが組み合わさってできている連結ロケットの分裂を考えます。ここで、小型ロケットの質量はmkg、大型ロケットの質量はMkg、連結ロケットの質量はM+m kgとなるとします。
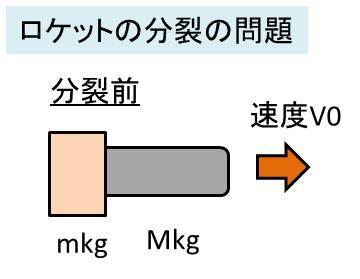
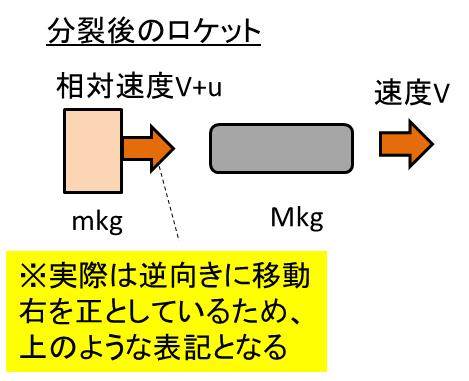
このとき、連結ロケットの初速度がV0であり、途中で速度を上げたいために小型ロケットを相対速度uでロケットの進行方向と逆向きに切り離したとします。このときの、分離後の大型ロケットの速さVについて考えていきましょう。
まずは、物体の分離前後のでの運動量保存則を立てていきます。
(M+m)Vo = MV + m(V+u) ・・・①となります。ここで、uが正の方向の逆となるために、負の値となることに気を付けましょう。
この式を整理して、ロケット分離後の速度V=の式に修正していきます。
①⇔ (M+m)Vo = (M+m)V + mu ⇔ (M+m)V = (M+m)Vo - mu ⇔ V = V0 - m/(M+m)uとなるのです。
ここで、uは負の値であるため、物体が分裂後の速度は初速度よりも大きくなります。これは直感的にもわかるでしょう。
今回はロケットという物体のの分裂の速度の問題を求めましたが、運動量保存則が成立する条件であれば、基本的に運動方程式の立式して、式中に相対速度を組み込むと解けます。
関連記事
弾性衝突と非弾性衝突
2物体が合体する際の計算問題を解いてみよう【片方が静止時の衝突の問題】
今度は2つの物体が合成されるときの、衝突前後の速度について解説していきます。
ある速度をVA(正の方向)で動いている質量Mの物体Aと、静止している質量mの物体Bとが、衝突したとします。このとき、2物体が合体し一体となった速度で移動するときの、この速度を計算していきましょう。
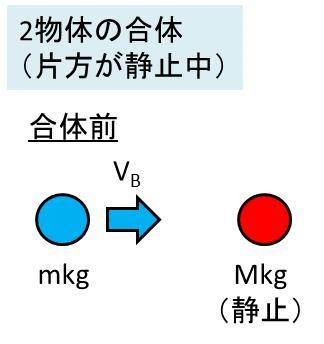
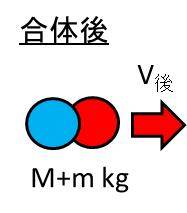
この2物体の合体の計算問題は、結局は物体の球の衝突の問題における非弾性衝突(反発係数e=0)のときの問題といえます。
先にも述べた手順の通り、運動量保存則の式を立てていきましょう。
M・0 + mVB = (M + m)V後 という運動方程式が立てられます。
よって、単純にV後=mVB/(M + m)となります。
関連記事
弾性衝突と非弾性衝突
両方が移動しているときの2物体が合体する際の計算問題を解いてみよう
それでは、同様に2物体が動いている際の合成時の速度も求めていきましょう。
ある速度をVA(正の方向)で動いている質量Mの物体Aと、同じ方向に速度VB(VA<VB)で移動している質量mの物体Bとが、衝突したとします。このとき、2物体が合体し、一体となった速度で移動するときの速度を計算していきましょう。
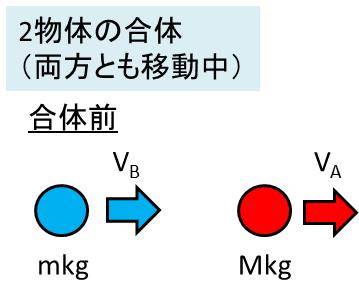

2物体の合体においても、MVA + mVB = (M + m)V後 となるため、こちらも単純にV後= MVA + VB / (M + m)となるのです。
このように、運動量保存則や相対速度の考え方を使用すると、ロケットなどの2つの物体が合体・分裂する際の速度を計算できることを覚えておきましょう。
関連記事
弾性衝突と非弾性衝突
ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】