物質波とブラッグ反射(ブラッグの式)
こちらのページでは
・物質波とは
・ブラッグの式・ブラッグ反射とは? 波長との関係
・ブラッグの式の計算問題を解いてみよう【演習問題】
について解説しています。
物質波とは
光は波としての性質も粒子としての性質も持っています(光の二重性)。
さらに光だけでなく、原子や電子などの粒子も同様に粒子としての性質だけでなく、波としての性質も持っています(電子の二重性)。
この粒子が持つ波としての性質のことを物質波、またはこの仮説を立てた学者であるド・ブロイさんの名前にちなんでド・ブロイ波とも呼ばれています。
さらに、波としての性質を持つ粒子の波長は λ = h/p = h/mv で表れます。
また、この波長λの値は非常に小さく、目視では確認できないレベルの大きさです(波長と電磁波の関係はこちらで解説しています)。

関連記事
光の二重性とは
波長と電磁波の関係
物質波(ドブロイ波)とハイゼンベルグの不確定性原理
光の二重性(粒子性と波動性)を結びつける式(波動関数)
ブラッグの式・ブラッグ反射とは? 波長との関係
また、粒子が波としての性質をあらわすことの実験の一つに波の干渉の性質を利用した実験があります。
これは、大学課程以降のある物質の構造解析でも使用されているXRD(X-Ray Diffraction)、X線回折
と呼ばれる実験装置の原理としても使われています。
この実験とはまず、結晶などの規則的にX線を反射する物質に対して、X線を照射し、その反射線の干渉の条件を見るという実験です(XRDの原理はこちらで解説しています)。
以下に実験のイメージ図を示します。
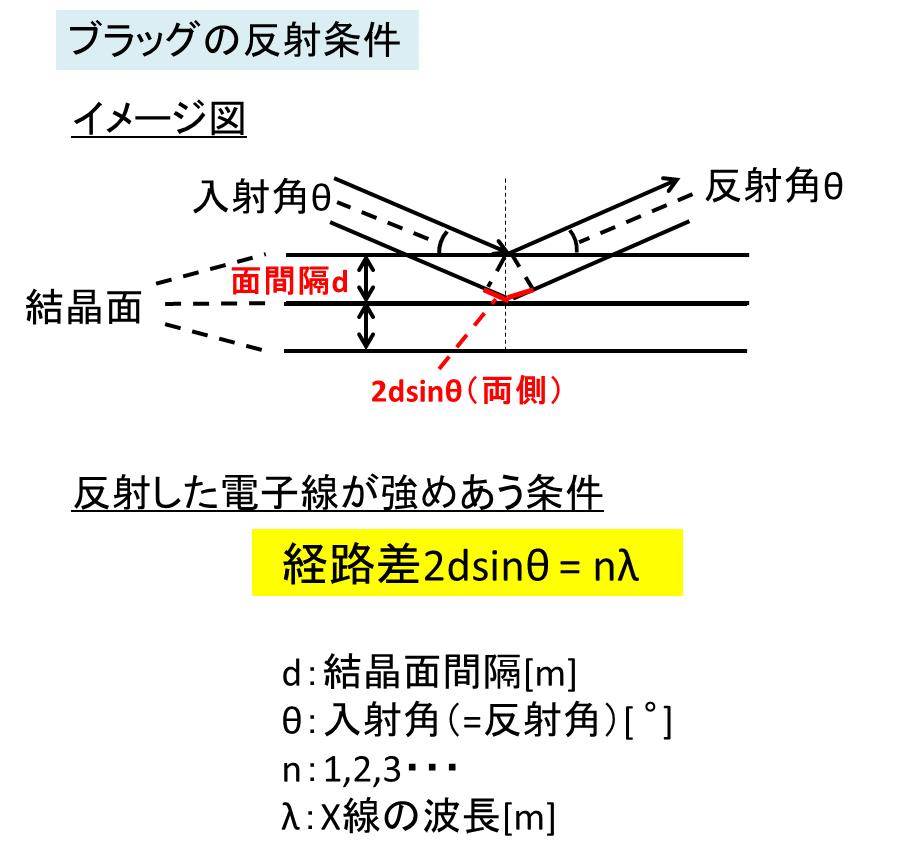
・結晶面に対して入射、反射するX線の角度をθ [°]
・結晶面の間隔(面間隔)をd[m]
・n=1,2,3・・・
・入射X線の波長[m]
とします。
この2dsinθ = nλ と結晶面と次の結晶面の経路差 2dsinθが波長のn倍(整数倍)であることを表した式をブラッグの式と呼びます。また、先にも述べた流れがブラッグの式の導出方法といえます。
また、このときにブラッグの式が成立しているときの角度のことをブラッグ角とよびます。同時に、結晶面によってX線や中性子線が散乱されることをブラッグ散乱と呼びます。
ブラッグの式においては、呼ばれる最も上の結晶面と次の結晶面の経路差 2dsinθが波長の整数倍(n倍)であると干渉(波長が強めあうこと)が起こります。ここで、dは面間隔を表しています。
この条件のことをブラッグの反射条件と呼びます。別の言い方では、「ブラッグの条件」「ブラッグの法則」などとよばれることもあります。
(XRDでは、基本的にθの2倍の値である2θ(回折角とよびます)を計測し、その半分の値のθをブラッグの式に当てはめます)
関連記事
XRDの測定原理と解析方法
XRDに使用するkα線、Kβ線とは
光の二重性とは
波長と電磁波の関係
物質波(ドブロイ波)とハイゼンベルグの不確定性原理
光の二重性(粒子性と波動性)を結びつける式(波動関数)
ブラッグの式の計算問題を解いてみよう【演習問題】
このようにブラッグの式の意味は、入射線と反射線の経路差がn倍(整数倍)のときに、波の干渉がおこることを示したものでした。
ただ、実際にはどのようにブラッグの式、ブラッグの反射条件を使用して計算するのでしょうか。
以下で、ブラッグの法則を使用し、各パラメータの求め方を考えていきましょう。
例題
あるシリコン結晶において面間隔、ピークが検出されている結晶面(ミラー指数)、ピークの強度がわかってるとします。
面間隔の値は314pm、波長0.1nmであったとします。このときの回折角2θを計算してみましょう。
解答
以下のブラッグ反射の定義をもとに計算していきます。

ここで、n=1のときを考えてみましょう。
すると、2 × 314×10^-12 × sinθ = 1 × 10^-10 よりsinθを算出しましょう。sinθ = 0.1592 となります。
ここで、エクセルや関数電卓を用いてsin-1関数を使用するとθ=9.16°となります。
(ちなみに、上述したシリコン結晶はp型半導体、n型半導体などの材料であったり、当サイトのメインテーマでもあるリチウムイオン電池の負極活物質(シリコン系)として注目されている材料です。
関連記事
p型半導体、n型半導体とは
負極活物質(シリコン系)
物質波とブラッグ反射(ブラッグの式) 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】