コンデンサーの静電エネルギーの式と単位 静電エネルギーの計算問題をといてみよう
こちらのページでは高校物理における電磁気学の中でも、コンデンサーに蓄えられるエネルギーに関する内容について解説していきます。
・コンデンサーの静電エネルギーの計算式1/2CV^2の導出方法
・コンデンサーを並列にした場合の合成容量の計算問題を解いてみよう
・コンデンサーに蓄積できるエネルギーを計算してみよう【演習問題】
にというテーマで解説しています。
・コンデンサーの静電エネルギーの計算式1/2CV^2の導出方法
結論からいいますと、コンデンサーに溜めることができるエネルギーの量は1/2CV^2=1/2QVで表すことができます。
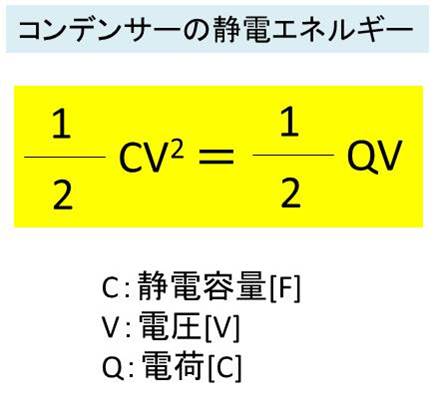
このコンデンサーで所持できるエネルギーのことを、静電エネルギーと呼びます。
それでは、この静電エネルギーはなぜ1/2CV^2=1/2QVという値になるのでしょうか。この理由について以下で確認していきます。
コンデンサーでは、電極間の電圧の大きさは低い段階では、その静電容量も小さいです。これは、溜まった電荷量Q=CVという関係式があるためです。
このとき、電場がかかった場所に電荷量qの電荷を配置したときのエネルギー(電気的な位置エネルギー)は、自身の電荷×電場に逆らって変化した電圧(電位差)(U=qVの式)で表すことができます。
コンデンサーでも、電荷が溜まりだすと、極板内に電場が生じるために、エネルギーが発生します。ただ、コンデンサーでは、直接電源によって電圧を印加した場合とは異なり、たまる電荷によって電圧も変動するのです。
つまり、電極へ移動した電荷が少ないときは電圧もひくく、時間の経過とともに電荷が大きく移動すると電圧が上昇していくのです。(とはいってもコンデンサーの充電は早くに終了しますが、実際はこのような反応が起こっているのです)。
この考え方を基に、横軸に電荷(Q)として、縦軸に電圧(V)をとったグラフを作成したとすると以下のようになるのです。
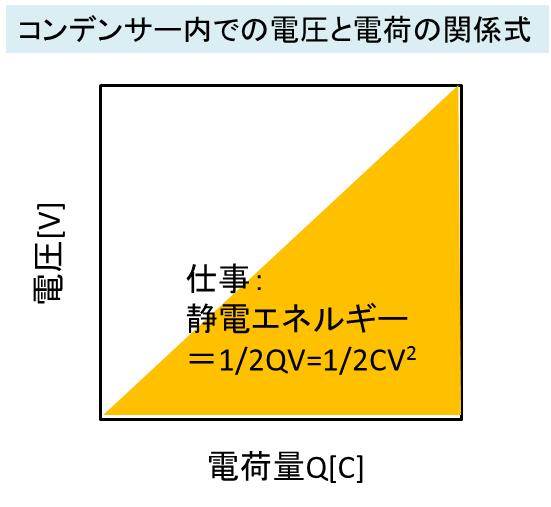
ここで、よってコンデンサーで所有できるエネルギーはこの面積に相当する1/2CV^2となるのです。
ここで、電荷と電圧の関係のQ=CVを代入すると、1/2QVとも変形できるため、コンデンサーのエネルギーは1/2CV^2もしくは、1/2QVと表すことが可能なのです。
関連記事
コンデンサーとは?コンデンサーの静電容量の式と導出方法
コンデンサーの直列合成
コンデンサーの並列合成
コンデンサーに蓄積できるエネルギーを計算してみよう【演習問題】
それでは、理解を深めるためにもコンデンサーの静電エネルギーの計算問題を解いてみましょう。
問題
外部電源により、電極間の電圧を3Vとして、十分に時間が経過したときの、コンデンサーのエネルギーを考えていきましょう。このとき、蓄えられている容量が2μFであるとします。
解答
上述の定義式に従い静電エネルギーを求めていきましょう。
すると、1/2CV2 = 1/2 × 2×10^-6 × 3×3 = 9× 10^-6 J =9μJ となります。
公式を忘れても大丈夫なように、導出方法自体を理解しておいた方がいいです。
関連記事
コンデンサーとは?コンデンサーの静電容量の式と導出方法
コンデンサーの直列合成
コンデンサーの並列合成
静電エネルギーの単位 ファラッドとジュールの違いは?
上記で、静電エネルギーの単位をJと記載しましたが、なぜ直接このように記載できるのでしょうか。以下で確認していきます。
まずファラッドF=C/Vであることから、静電エネルギーの単位は [C/V]×[V^2] = [CV] = [J] と変換できるわけです。
このとき、静電容量を表す記号であるCと単位のC(クーロン)が混ざらないように気を付けましょう。
関連記事
ジュール・クーロン・ボルトの単位変換方法
コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】