コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】
こちらのページでは高校物理における電磁気学の中でも、コンデンサーの性質に関する内容について解説していきます。
・コンデンサーとは何か?
・コンデンサーの静電容量の式【容量の電荷・電圧との関係】
・電気力線の考え方からコンデンサーの静電容量を導出する方法
について解説しています。
コンデンサーとは何か?
ある異なる二つの物体をこすり合わせると、帯電により
片方の物体には正の電荷がたまり、もう片方には負の電荷がたまります。
正、負の電荷の対が存在するということは電気エネルギーをためていることであり、
このような原理を用い、電荷を貯められるよう装置のことをコンデンサーと呼びます。
(※高校物理の範囲から外れますが、実用化されている電気二重層コンデンサー等の
各種コンデンサーについてこちらで解説しています。)
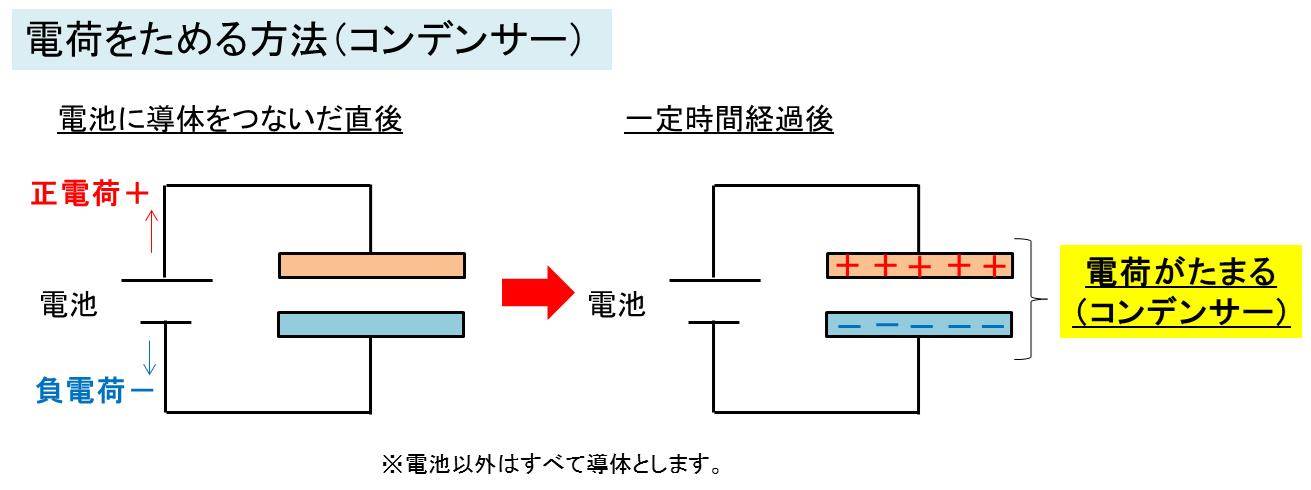
二つの物体をこすり合わせる方法ではなく、電荷をためる方法としては、
下図のよう電池のプラス極に導体をつないだもの(導体1)と、
電池のマイナス極を導体でつないだもの(導体2)を近づける方法があります。
プラスとマイナス極が近くに存在するため引力により引き付けられている状態となり、
電池を外してもこの状態が保たれます。
高校物理では、下図のように平板上のコンデンサーモデルを扱い、下記に解説していきます。
(※高校物理の範囲から外れてしまいますが、電池とコンデンサーは別物であり、
一般的に電池の方が容量が大きいのですが充放電の速度(Cレートや時間率)が遅く、
逆にコンデンサーは容量が小さいのですが充放電の速度(Cレートや時間率)が非常に速い
という特徴を持ちます。)
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーの直列接続時の合成容量
コンデンサーの並列接続時の合成容量
ファラド、クーロン、ボルトの変換方法
コンデンサーの静電容量の式【容量の電荷・電圧との関係】
コンデンサーの性能を表すパラメータの一つとして、容量が挙げられます。
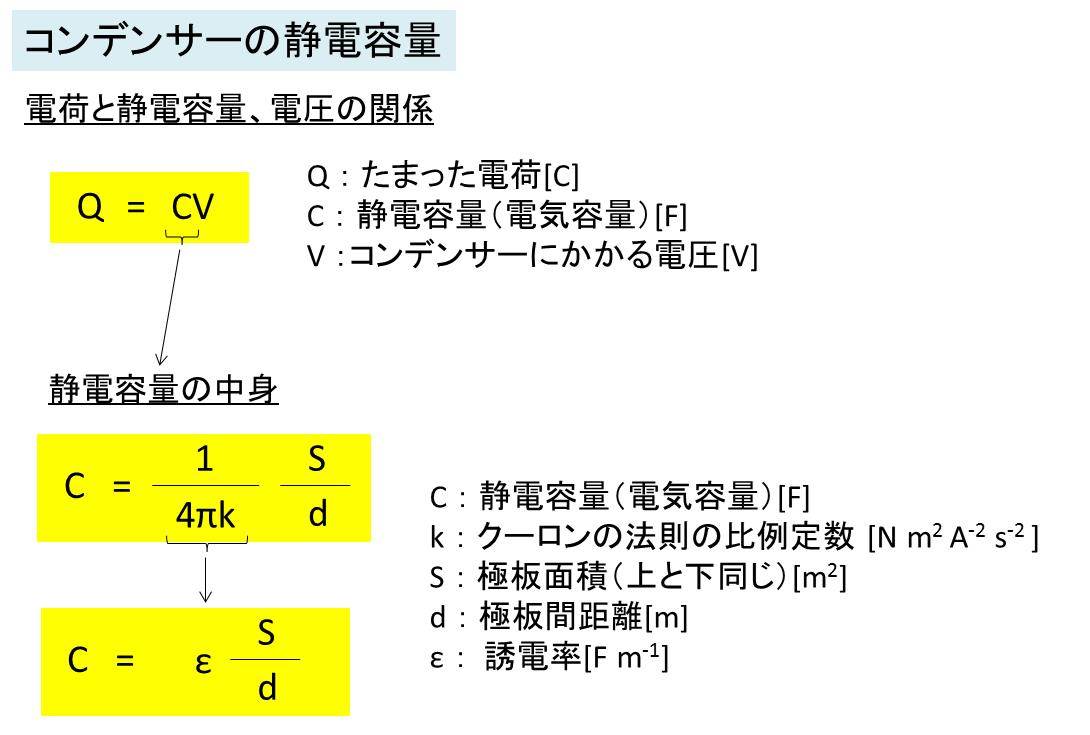
コンデンサーにたまった電荷(ためられる電荷)、静電容量
(単に容量、電気容量と呼んだりします)、電圧の関係は以下の式で表されます。
上にまとめは記載しましたが、簡単にポイントを解説します。
コンデンサーにたまった電荷(ためられる電荷)Qは、
静電容量Cとコンデンサーにかかる電圧Vの積(つまりQ=CV)で表すことが出来ます。
そして、静電容量Cの中身を見ていきますと、
C = 1/4πk × S/d で表すことができます。
さらに、1/4πk は誘電率ε(イプシロン)と呼ばれる物質特有の値にも置き換えられるため、
C = ε × S/dとも表すことができます。
つまり、静電容量はコンデンサーの極板面積Sに比例し、極板距離dに反比例します。
よって、極板面積Sを大きくし、極板距離dを小さくする(狭くする)ことで、静電容量を大きく、
つまりためられる電荷の量を大きくすることができます。
また、静電容量Cの単位は[F(ファラッド)]と呼びますが、実用化されているセラミックコンデンサーや電気二重層コンデンサー(電気二重層キャパシタ)では、μFやpFで表されることが一般的です。
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーの直列接続時の合成容量
コンデンサーの並列接続時の合成容量
ファラド、クーロン、ボルトの変換方法
電気力線の考え方からコンデンサーの静電容量を導出する方法)
コンデンサーにためられる電荷はQ = CVで表され、かつ>C = 1/4πk × S/dとも表すことができることを上で解説しました。
ここでなぜ、このようにC = 1/4πk × S/dで表されるのかを電気力線の定義に戻り考えていきます。
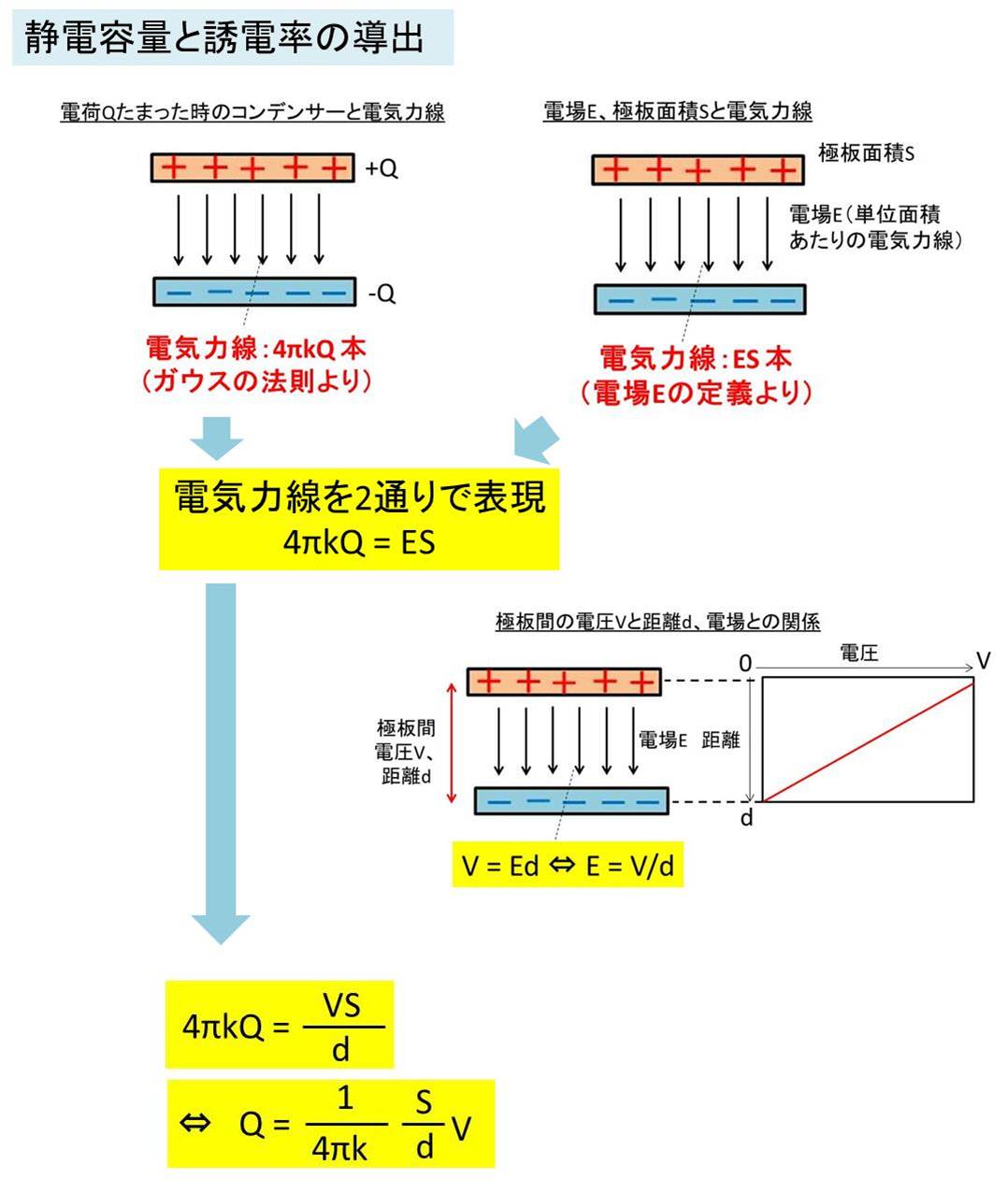
下記フローにおいて、左上図では、コンデンサーに電荷Q[C]たまった際(正電荷が+Q[C]、負電荷が-Q[C]たまった状態)の電気力線の本数はガウスの法則より、電気力線の本数 = 4πkQ [本]です。
次に、電場つまり1m^2辺りの電気力線の本数をEとし、コンデンサーの極板面積をS[m^2]とすると電気力線の本数 = ES [本]とも表されます。
これらは同じ意味で別の表現をしているだけであるため、4πkQ = ES が成り立ちます。
さらに、コンデンサ-にかかる電圧V = Ed の関係式を変形し、 E = V/dを上式に代入すると、
C = 1/4πk × S/d を導出でき、さらに Q = 1/4πk × S/d × V となります。
これらの導出の流れは入試等で良く見かけるので、きちんと理解しておきましょう。
関連記事
直列時の合成抵抗
並列時の合成抵抗
コンデンサーの直列接続時の合成容量
コンデンサーの並列接続時の合成容量
コンデンサーの容量の計算式と導出方法【静電容量と電圧・電荷の関係式】 関連ページ
- SI単位
- 密度とは?比重とは?密度と比重の違いは?【演習問題】
- ミリ、ミクロン、ナノ、ピコとは?SI接頭語と変換方法【演習問題】
- 電位とは何?電位の定義は?
- 電気と電荷、静電気力
- 電流と電荷(I=Q/t)、電流と電子の関係
- コンデンサーと交流
- 電圧とは何か?電圧のイメージ、電流と電圧の関係(オームの法則)
- 直列回路における合成抵抗の導出と計算方法【演習問題】
- 並列回路における合成抵抗の導出と計算方法【演習問題】
- 合成抵抗2(直列と並列が混ざった回路)
- 電力と電力量の違いは?消費電力kWと消費電力量kWhとの関係 WとWhの変換(換算方法) ジュール熱の計算方法
- ジュール熱とは?ジュール熱の計算問題を解いてみよう【演習問題】
- 水の温度上昇とジュールの関係は?計算問題を解いてみよう【演習問題】
- コンデンサーを直列接続したときの静電容量の計算方法【演習問題】
- コンデンサーを並列接続したときの静電容量の計算方法【演習問題】
- コンデンサーのエネルギーが1/2CV^2である理由 静電エネルギーの計算問題をといてみよう
- 磁場とは何か?
- 電流と磁場の関係(電流がつくる磁場)
- 電流が磁場から受ける力(フレミング左手の法則)
- ローレンツ力
- 電磁誘導とレンツの法則
- ファラデーの電磁誘導の法則
- 各種電磁誘導の問題の演習
- 磁束と磁束密度の定義・違いは?
- 相互誘導と自己誘導(相互インダクタンスと自己インダクタンス)
- コイルを含む回路、コイルが蓄えるエネルギー
- 直流と交流、交流の基礎知識 実効値と最大値が√2倍の関係である理由は?
- 抵抗、コンデンサーと交流抵抗、コンデンサーと交流
- コイルと交流、交流のまとめ
- 光のエネルギー
- 物質波とブラッグ反射(ブラッグの式)
- 気体分子運動論とは?
- 気体分子運動論とボルツマン定数
- 電流の定義のI=envsを導出する方法
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】
- クーロンの法則 導出と計算問題を問いてみよう【演習問題】
- 電気回路に短絡している部分が含まれる時の合成抵抗の計算
- 角速度(角周波数)とは何か?角速度(角周波数)の公式と計算方法 周期との関係【演習問題】(コピー)
- 自由落下(自然落下)における速度は? 計算問題を解いてみよう【演習問題】
- ばね定数の公式や計算方法(求め方)・単位は?ばね定数が大きいほど伸びにくいのか?直列・並列時のばね定数の合成方法
- 距離(位置)、速度、加速度の変換方法は?計算問題を問いてみよう
- 静止摩擦係数と動摩擦係数の求め方 静止摩擦力と動摩擦力の計算問題を解いてみよう【演習問題】
- 電流計は直列につなぎ、電圧計は並列につなぐのはなぜか 電流計・電圧計の使い方と注意点
- 抵抗が3つ以上の並列回路、直列回路の合成抵抗 計算問題をといてみよう
- 単振動における変位・速度・加速度を表す公式と計算方法【sin・cos】
- ホイートストンブリッジにおける計算問題を解いてみよう【ブリッジ回路の解き方】
- メートルブリッジの計算問題を解いてみよう【ブリッジ回路の解き方】
- 単振動における運動方程式と周期の求め方【計算方法】
- 単振動におけるエネルギーとエネルギー保存則 計算問題を解いてみよう
- v-tグラフ(速度と時間の関係式)から変位・加速度を計算する方法【面積と傾きの求め方】
- 相対速度とは?相対速度の計算問題を解いてみよう【船、雨、0となるときのみかけの速度】
- ロケットなどで2物体が分裂・合体する際の速度の計算【運動量保存と相対速度】
- キルヒホッフの電流則(キルヒホッフの第一法則)とは?計算問題を解いてみよう
- 単振り子における運動方程式や周期の求め方【単振動と振り子】